Numerický výpočet ocelového prvku se styčníky
Zúčastnili jsme se studentské konference Zapálení 2025 a společně s organizátory vybrali několik zajímavých prací. Ing. arch. Petr Hejtmánek, Ph.D. doporučil níže uvedený text s tím, že výsledky výpočtu se velmi dobře shodují s experimentem a jsou doplněny citlivostní studií, která rozšiřuje využitelnost výsledků v praxi.
Úvod
Ocelové styčníky musí být v konstrukci spolehlivé jako její prvky. Zajišťují efektivní přenos vnitřních sil. Jejich selhání může mít kritičtější následky než selhání prvků. Při návrhu požární odolnosti na základě globální analýzy za běžné teploty se jejich posouzení za požáru neprovádí. Předpokládá se, že za běžné teploty dobře navržené vyhovují i během požáru, pokud jsou požárně chráněny alespoň tak jako připojované prvky. Přístup je založen na předpokladu větší koncentrace materiálu v místě spoje, což způsobí pomalejší ohřev, tedy kritické teploty zde bude dosaženo později než v nosném prvku. Zmíněné řešení nemusí být vždy dostačující. Opomíjí například polohu styčníku nebo změnu namáhání. Práce navazuje na disertační práci Der Batuhan [1], který metodu CBFEM za zvýšené teploty připravil, validoval a verifikoval na řadě příkladů.
Metoda konečných prvků s komponentami
Metoda CBFEM je v současnosti běžně využívána v praxi pro výpočet ocelových styčníků za běžné teploty a je zahrnuta například v softwarech od společností IDEA StatiCa nebo Dulbal. Již z názvu je jasné, že se jedná se o kombinaci analytické metody komponent (MK) a metody konečných prvků (MKP). Stejně jako v MK se styčník rozdělí na jednotlivé komponenty. K MKP modelování plechů se obvykle využívají skořepinové prvky pro rychlost výpočtu. Ve výpočtu zpřesní působení vnitřních sil uvažováním tuhosti plechů. Ostatní komponenty jako šrouby a svary jsou reprezentovány nelineárními pružinami a posouzeny v souladu návrhovými normami, v Česku např. s ČSN EN 1993-1-8. [2, 3]
Experiment
Pro studii byla vybrána práce od Khalifa Saif Al-Jabri z Univerzity v Sheffieldu [4]. Zkoušelo se 11 konfigurací ocelových styčníků rozdělených do tří skupin. Zkoušené vzorky byly vždy symetrické: sloup byl 2,7 m vysoký. Dva nosníky o délce 1,9 m byly symetricky připojeny čelními styčníkovými plechy. V podlažních ocelových stavebních konstrukcích se jedná o nejčastější přípoj. Skupiny se odlišovaly ocelí, velikostí průřezu a tuhostí.
Při zkoušce se za zvýšené teploty vyhodnocovala závislost pootočení na ohybovém momentu. Během zkoušek byl vzorek vystaven konstantnímu zatížení pomocí hydraulického lisu 1,5 m od osy sloupu. Teplota plynu byla lineárně zvyšována přírůstkem 10 °C za min. Byla využita pec s plynovými hořáky. Nejvyšší teplota konstrukce byla 900 °C.
Sloupu bylo během zkoušek u podlahy zabráněno vodorovným a svislým posunům. Horní uchycení svislý posun umožnilo. Podobně byly zajištěny i nosníky. Na jejich koncích byl umožněn pouze vertikální posun.
V této práci byla vybrána zkouška z první skupiny, třetí se zatížením 13 kNm. Sloupy byly průřezu 152×152×23UC a nosníky 254×102×22UB. Styčníkový plech 130 mm × 265 mm × 8 mm je přivařen k nosníku 4mm koutovými svary. Ke sloupu připojen šesti šrouby M16 8.8. Veškerá ocel je třídy oceli 43, což odpovídá dnešní S275, s kterou uvažuji později ve výpočtu.
Numerický výpočet
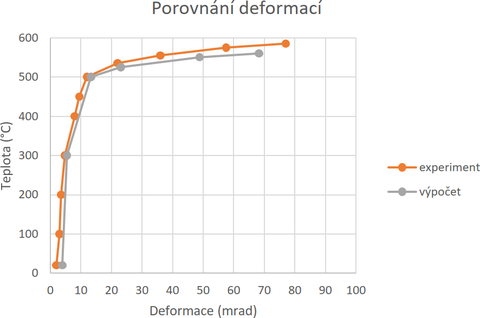
Výpočetní model přesně kopíruje geometrii a zatížení při experimentu. Standardní verze programu IDEA StatiCa Connection ve verzi 24.1 neodečítá přesné hodnoty deformací. Pro účel této práce byla poskytnuta technickou podporou upravená verze, ve které je funkce dostupná. Při výpočtu se postupovalo s nárůstem teploty v dílčích krocích. Výsledky výpočtu jsou zobrazeny na obrázku 3.
Validace
Na první pohled z grafu na obrázku 3 je vidět, že numerickým výpočtem lze u tohoto experimentu dosáhnout dobré předpovědi chování. V tabulce 1 jsou uvedeny změřené a vypočtené hodnoty natočení v průsečíku os ve styčníku, jejich rozdíl a odchylky. Velká počáteční neshoda 42 % je pravděpodobně způsobena dotvarovánín vlivem výrobních imperfekcí.
| Deformace [mrad] | Experiment [°C] | Výpočet [°C] | Experiment − výpočet [°C] | Experiment/výpočet [–] |
|---|---|---|---|---|
| 5 | 306 | 216 | 90 | 42 % |
| 10 | 460 | 416 | 44 | 11 % |
| 20 | 528 | 517 | 11 | 2 % |
| 30 | 546 | 532 | 14 | 3 % |
| 40 | 559 | 541 | 18 | 3 % |
| 50 | 568 | 551 | 17 | 3 % |
| 60 | 576 | 556 | 20 | 4 % |
| 68,25 | 578 | 560 | 18 | 3 % |
Studie citlivosti
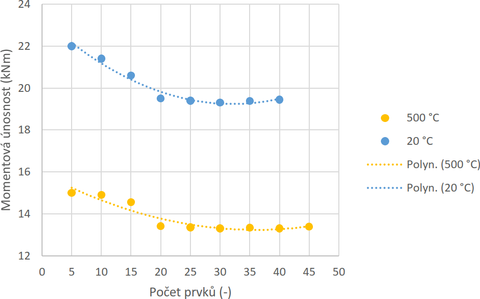
Na řešeném příkladu byla připravena studie vlivu sítě, umístění šroubů, tloušťky čelní desky a svarů na momentovou únosnost.
Software volí vhodné rozměry sítě automaticky. Jemnost sítě je u každého numerického výpočtu zásadní. Počet prvků byl postupně zvedán vždy po pěti a sledovala se únosnost konstrukce při teplotě 20 °C a 500 °C. V obou případech došlo k ustálení hodnoty únosnosti okolo 25 prvků, obrázek 4. Programem navržená hustota sítě o osmnácti prvcích je vhodná.
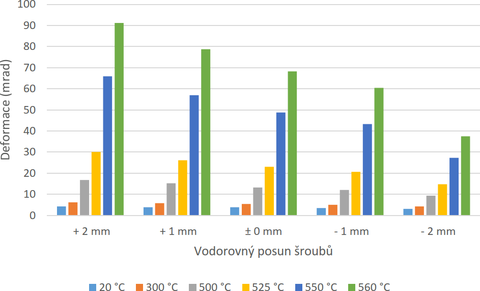
Obr. 5 Graf citlivosti na vodorovném posunu šroubů
Fig. 5 Graph of sensitivity to horizontal screw displacement
Intuitivně se předpokládá, že posunutím šroubů do tažené oblasti styčníku a zvětšení ramene vnitřních sil umožní zmenšení deformace. U tohoto styčníku má na únosnost větší vliv jejich posunutí blíže ke stojně nosníků a zvýšení tuhosti T průřezu, viz obrázek 5.
Závěr
Cílem práce byla validace modelu metodou CBFEM, ze které vyplývá, že numerickým výpočtem lze získat dobrou předpověď odezvy styčníku na zatížení i za zvýšené teploty. Validovaný výpočet bude podkladem pro diplomovou práci, která se zaměří na vliv mezní poměrné deformace plechu a svarů a mezní protažení šroubů na předpověď únosnosti tohoto styčníku. Předpokládá se experimentální ověření mezního poměrného přetvoření konstrukční oceli za zvýšené teploty při konstrukci odpovídající koncentraci napětí ve vrubech.
Literatura
- BATUHAN, Der. Numerical calculation of members and joints at elevated temperature. B.m., 2024. Doctoral thesis. České vysoké učení technické.
- Teoretické základy. In: [online]. B.m.: IDEA StatiCa, nedatováno. Dostupné z:
https://www.ideastatica.com/cz/podpora/general-theoretical-background#Steel-connection-material-model - WALD, F. Component-based finite element design of steel connections. In Prague: Czech Technical University, 2020. ISBN 978-80-01-06702-4.
- KHALIFA SAIF, Al-Jabri. The behaviour of steel and composite beam-to-column connections on fire. B.m., 1999. Doctoral thesis. University od sheffield.


Oceněný studentský článek v rámci konference ZAPÁLENÍ 2025.
Řešení požární odolnosti ocelových prvků v reálné praxi většinou nezahrnuje posouzení vlivu styčníků na požární odolnost ocelových konstrukcí. Selhání styčníků při namáhání požárem může mít fatální následky na konstrukci jako celek. Většinou se předpokládá, že styčníky za běžných teplot požáru vyhovují požadavkům, pokud jsou chráněny proti účinkům požáru stejně jako připojované prvky. Vychází se z předpokladu, že v místě styčníkového spoje je větší koncentrace materiálu, kritické teploty bude tedy dosaženo později než v připojovaném prvku. Opomíjeny jsou další možné vlivy, které zahrnují např. geometrickou polohu styčníku, možné změny namáhání konstrukce i styčníku za požáru atd.
Pro výpočet namáhání styčníku za běžných teplot se v dnešní praxi běžně používá metoda CBFEM. Autor článku provedl validaci modelu metodou CBFEM pro ověření namáhání styčníku za zvýšené teploty. Ze závěru článku vyplývá, že numerickým výpočtem lze získat dobrou předpověď odezvy styčníku na zatížení i za zvýšené teploty. Uvedené konstatování je cenným poznatkem pro podrobnější zkoumání problematiky chování styčníků ocelových konstrukcí při namáhání požárem.
Závěr: článek doporučuji k vydání.
The paper deals with the numerical calculation of a steel joint at elevated temperature. The Sheffield experiment, well known and described in the literature, has been studied. The study of the shell model has been carried out using the (CBFEM). The validation of the model shows good agreement with the experiment. A summary of the sensitivity study is included in the paper.

![Obr. 1 Fotografie z vybrané zkoušky [4]. Fig. 1 Photos from the selected exam [4]](/docu/clanky/0288/028827o2.jpg)
![Obr. 2 Výkres vybraného styčníku [4]. Fig. 2 Drawing of the selected connector [4]](/docu/clanky/0288/028827o4.png)