Vzpěrné délky ocelových oblouků. Část 1: Dvojkloubové a vetknuté oblouky
Uvedeny jsou výsledky rozsáhlé studie týkající se vzpěrných délek kruhových ocelových oblouků. Studie v Části 1 pokrývá oblouky dvojkloubové a vetknuté, v Části 2 oblouky trojkloubové s vrcholovým kloubem vidlicovým (pouze v rovině oblouku) a trojkloubové oblouky s vrcholovým kloubem úplným (v rovině i z roviny oblouku). Všechny studie jsou provedeny pro tři typy rovnoměrného zatížení (svislé po délce oblouku, svislé na půdorys oblouku a zatížení radiální). Hodnoty vzpěrných délek ekvivalentního přímého (Eulerova) prutu s konstantní osovou silou odpovídající maximální osové síle v patce oblouků jsou uvedeny ve formě grafů pro uzavřené trubkové průřezy, pro různé otevřené válcované průřezy IPE a různé širokopřírubové průřezy HEB. Studie navazuje na článek autora Stabilita ocelových kruhových oblouků [1], obsahující úvodní stabilitní analýzu dvojkloubových oblouků.
1. Úvod
Stabilitní chování dvojkloubových ocelových kruhových oblouků popsal autor v příspěvku [1], kde jsou uvedeny jednoduché přístupy k posouzení těchto konstrukcí při běžném návrhu. Při obvyklém pružném návrhu lze postupovat podle doporučení Eurokódů (ČSN EN 1993-1-1, kap. 5.2 „Globální analýza“ a ČSN EN 1993-2, Příloha D.3).
Geometricky nelineární analýza s imperfekcemi (GNIA) vyžaduje zavedení správného tvaru a velikosti počátečních průhybů (popř. též reziduálních pnutí po průřezu). Průběh počátečních průhybů je však komplikovaný, tvary uvedené v ČSN EN 1993-2 jsou spíše nesprávné (vesměs neodpovídají kritickým tvarům při vybočení v rovině a z roviny oblouku, popř. jen přibližně). Naopak jednoduchý výpočet pomocí lineární analýzy (LA) ideálního oblouku ve spojení s lineární bifurkační analýzou (LBA), tedy po zavedení vzpěrné délky, převádí pomocí součinitelů vzpěrnosti posouzení na ekvivalentní imperfektní Eulerův prut s odpovídajícím počáteční průhybem a reziduálním pnutím. Následující posouzení s dalšími vnitřními silami podle Eurokódu zahrnuje potřebné interakce.
Úvodní studie pro dvojkloubové oblouky [1] prokázala, že hodnoty vzpěrných délek stanovených ve 3D závisí na tuhostních parametrech průřezu oblouku, zejména pro vybočení z roviny oblouku. Současná studie uvádí vzpěrné délky pro vybočení v rovině i z roviny oblouku v grafech na základě LBA, plynoucích z parametrické studie 560 případů. Pokrývá dvojkloubové, vetknuté a trojkloubové oblouky (s vidlicovým nebo úplným vrcholovým kloubem) pro tři typy zatížení, 7 různých průřezů (vesměs tužších pro vybočení v rovině oblouků) a pět poměrů H/L (vzepětí k půdorysné délce oblouku). Pro rovnoměrná zatížení a odpovídající proměnnou osovou sílu oblouku jsou vzpěrné délky vždy vztaženy k maximální osové síle v patě oblouku, která vstupuje do posouzení ekvivalentního základního (Eulerova) prutu daného průřezu.
Oproti úvodní studii zde již nejsou řešeny oblouky s kloubovým uložením pro vybočení z roviny oblouku, neboť takové uspořádání je nepraktické a v článku se proto uvažuje pouze kloubové uložení vidlicové (resp. čepové). Je na místě rovněž podotknout, že volně stojící oblouky jsou spíše výjimečné, neboť pro příčné zatížení musí být náležitě dimenzovány (jako „balkonové oblouky“) a obvykle jsou proto příčně ztuženy (uváděné vzpěrné délky pro vybočení z roviny se neuplatní).
2. Zásady pro stanovení vzpěrných délek oblouků
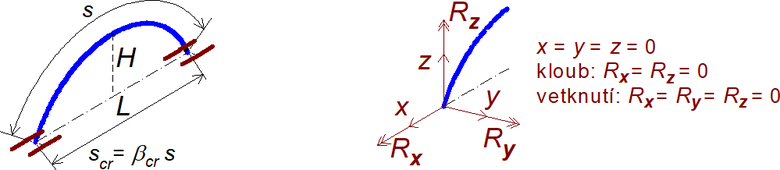
Pro kritická zatížení oblouků byla použita 3D LBA v programu SCIA Engineer (verze 20.0). Parametrická studie zahrnuje základní geometrii s vidlicovým uložením podle obr. 1 (L = 10 m, 145 uzlů na oblouku, 6° volnosti, přímý řešič Lanczos, 50 vlastních tvarů). Součinitele vzpěrné délky záleží na poměru H/L, nikoliv na rozpětí L.
Obr. 1 Základní geometrie a podmínky posuvu a rotace v podporách oblouků
Obecně lze pro prut délky (s) zatížený osovou silou N a obecné okrajové podmínky určit v LBA nejnižší kritické zatížení Ncr = αcr N a vzpěrnou (kritickou) délku scr stanovit jako délku stejně zatíženého základního (Eulerova) kloubově uloženého prutu se stejným kritickým zatížením. Pro součinitel vzpěrné délky βcr proto platí:
(1)
kde Eulerova kritická síla NE vztažného tlačeného prutu délky (s) při zatížení konstantní osovou silou je:
(2)
Ve vztahu (2) se zavede pro vybočení v rovině oblouku moment setrvačnosti průřezu Iy (obvykle k tuhé ose) a pro vybočení z roviny oblouku moment setrvačnosti průřezu Iz (obvykle k měkké ose).
Pro zatížení proměnnou osovou silou je kritická síla NE,v vyšší než pro zatížení silou konstantní NE (s obdélníkovým průběhem). U vyšetřovaných oblouků lze přibližně předpokládat lineární průběh osové síly s maximem v podporách a minimem ve vrcholu oblouku (zatímco skutečný průběh je nelineární a ve vrcholu hladký). Při převodu na Eulerův základní prut se předpokládá úsek oblouku s vybočením v jedné sinusové polovlně. Tomu odpovídá polovina délky oblouku při kloubovém uložení s trapezoidním průběhem osové síly, zatímco při vetknutí v rovině oblouku a vidlicovém uložení v podporách pro vybočení z roviny oblouku je to dvojnásobný úsek mezi podporou a inflexním bodem deformace (odpovídající průběh osové síly je ve tvaru D), obr. 2. Při kloubovém uložení z roviny oblouku odpovídá vybočení z roviny celé délce oblouku a průběh osové síly je přibližně ve tvaru K (tento případ byl řešen též ve článku [1]).
Obr. 2 Průběh osové síly v úseku oblouku
Kritická zatížení pro všechny uvedené průběhy proměnné osové síly N byla řešena v programu SCIA Engineer. Výsledky lze zapsat ve formě poměru kritického zatížení s konstantní normálovou silou (Eulerova) a s proměnnou osovou silou:
Průběh N ve tvaru T:
(3)
Průběh N ve tvaru D:
(4)
Průběh N ve tvaru K:
(5)
Odtud kritické zatížení prutu s proměnným zatížením lze obecně vyjádřit jako:
(6)
kde podle tvaru průběhu N je δi rovno δT, δD nebo δK.
Výpočtem kritického zatížení oblouků ve 3D byla získána kritická zatížení pro vybočení v rovině (Ncr,y) i z roviny oblouků (Ncr,z). Pro součinitel vzpěrné délky převádějící kritické zatížení oblouku s danou proměnnou osovou silou Ncr na Eulerův prut s konstantní osovou silou je nutné vybrat vhodný průřez – např. v patě oblouku s osovou silou Nmax. Odtud lze pro součinitel vzpěrné délky oblouku psát:
(7)
Součinitel βmax zde odpovídá prutu s konstantní osovou silou rovnou síle v patce oblouku a součinitel δi převádí hodnotu součinitele na příslušný proměnný průběh osové síly po délce oblouku.
Upozornění: Obdobně jako v [1] je vzpěrná délka oblouku scr vztažena k celé délce oblouku (s) jak pro vybočení v rovině, tak i z roviny oblouku (oproti např. mostní normě ČSN EN 1993-2/2007, kde pro vybočení v rovině oblouku je součinitel vzpěrné délky pro vybočení v rovině oblouku vztažen k poloviční délce oblouku s/2 a pro vybočení z roviny oblouku k celé půdorysné délce L. Přepočet na uvedené hodnoty lze provést podle vztahu (1)).
3. Parametrická studie oblouků
Kritická zatížení a vzpěrné délky oblouků byly řešeny pro 4 okrajové podmínky: dvojkloubový oblouk s vidlicovým uložením, vetknutý oblouk, trojkloubový oblouk s vidlicovým uložením a vidlicovým vrcholovým kloubem a trojkloubový oblouk s plným vrcholovým kloubem. Studie pokrývá 5 vztažných poměrů vzepětí k výšce oblouku: H/L ∈ < 0,1; 0,5 >. Kritická zatížení oblouků ve 3D jsou závislá na tuhostních parametrech průřezu oblouku. Pro vybrané uzavřené průřezy (všechny kruhové trubky) a otevřené válcované průřezy IPE a HEB platí Tab. 1. Studie převážně předpokládá tužší průřez pro vybočení v rovině oblouku („na stojato“), kde Iz je moment setrvačnosti pro vybočení z roviny oblouku a IT moment setrvačnosti v prostém kroucení.
| trubky | IPE120 | IPE300 | IPE450 | HEB120 | HEB300 | HEB450 | |
|---|---|---|---|---|---|---|---|
| Iz /Iy | 1 | 0,093 | 0,072 | 0,050 | 0,367 | 0,340 | 0,147 |
| Iz /IT | 0,5 | 15,9 | 30,0 | 25,1 | 23,0 | 46,3 | 26,6 |
| Iy /IT | 0,5 | 364,0 | 415,3 | 504,6 | 109,0 | 136,1 | 181,4 |
4. Vzpěrné délky dvojkloubových oblouků
(vztažené k osové síle v patě Nmax)
4.1 Zatížení po délce oblouku
4.1.1 Trubky a otevřené průřezy „na stojato“
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 3. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 2. Hodnota Nmin pro δT je stanovena v s/2 a pro δD v s/4.
Obr. 3 Příklad dvojkloubového oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,982 | 0,942 | 0,897 | 0,858 | 0,825 |
| √δD | 0,987 | 0,958 | 0,926 | 0,899 | 0,876 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 4.
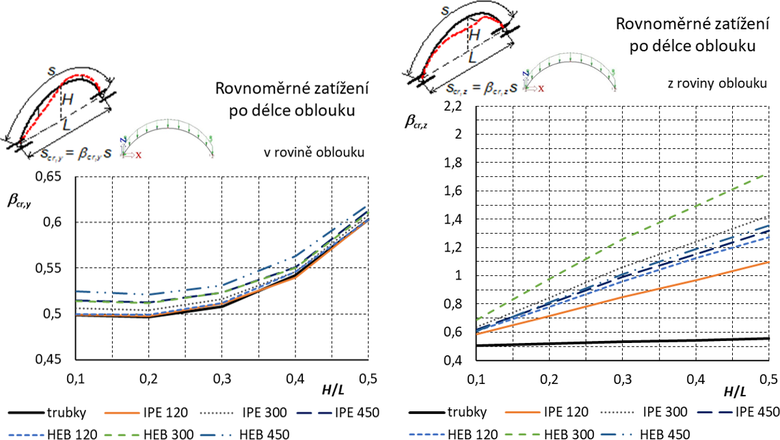
Obr. 4 Dvojkloubový oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
4.1.2 Trubky a otevřené průřezy „na ležato“
Vliv poměru momentu setrvačnosti k momentu v prostém kroucení (Iz /IT) je pro vybočení oblouku z roviny rozhodující (viz obr. 4). Pro stejné zatížení proto byla provedena studie s průřezem „na ležato“, kde uvedené poměry jsou mnohonásobné (viz Tab. 1, uplatní se poměry ve třetím řádku Iy /IT). Pro jinak stejné parametry, zatížení, reakce a převodní součinitele byly stanoveny součinitele vzpěrných délek podle obr. 5. Je zřejmé, že součinitele pro vybočení v rovině oblouku nyní splývají se součiniteli pro trubky, pro vybočení z roviny jsou však ve srovnání se součiniteli vzpěrných délek pro průřezy orientovanými „na stojato“ mnohem vyšší. Pro další typy zatížení dvojkloubových oblouků je situace obdobná a poloha „na ležato“ není uváděna.
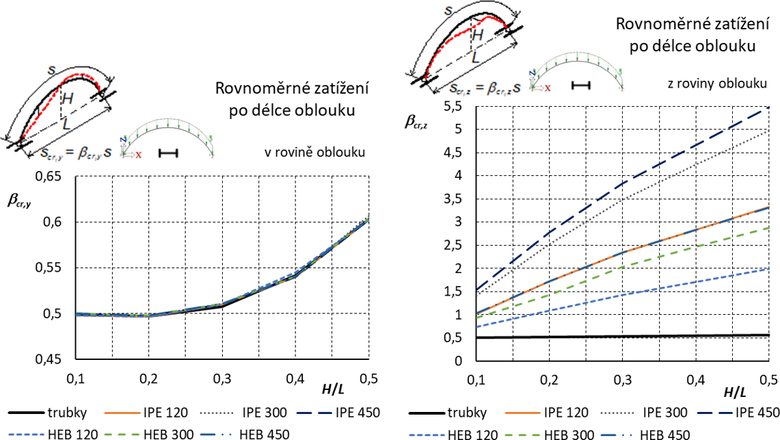
Obr. 5 Dvojkloubový oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na ležato“
4.2 Zatížení na půdorys oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 6. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 3. Hodnota Nmin pro δT je stanovena v s/2 a pro δD v s/4.
Obr. 6 Příklad dvojkloubového oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,983 | 0,946 | 0,909 | 0,877 | 0,849 |
| √δD | 0,987 | 0,961 | 0,934 | 0,912 | 0,893 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 7.
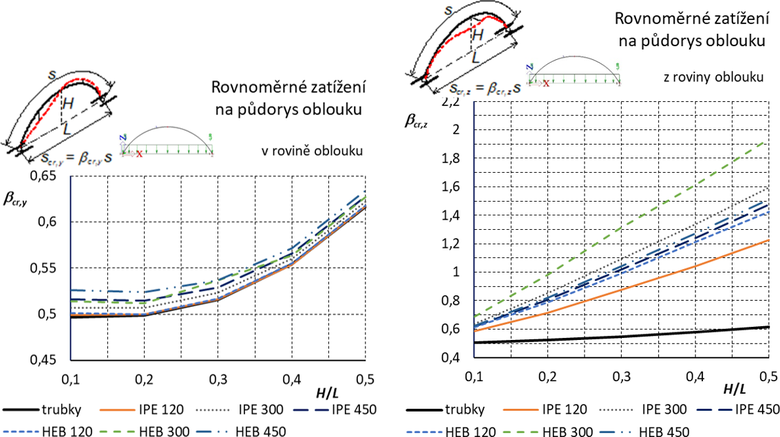
Obr. 7 Dvojkloubový oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
4.3 Radiální zatížení oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 8. Protože osová síla v oblouku je konstantní, pro převodní součinitele platí δT = δD = 1.
Obr. 8 Příklad dvojkloubového oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 9.
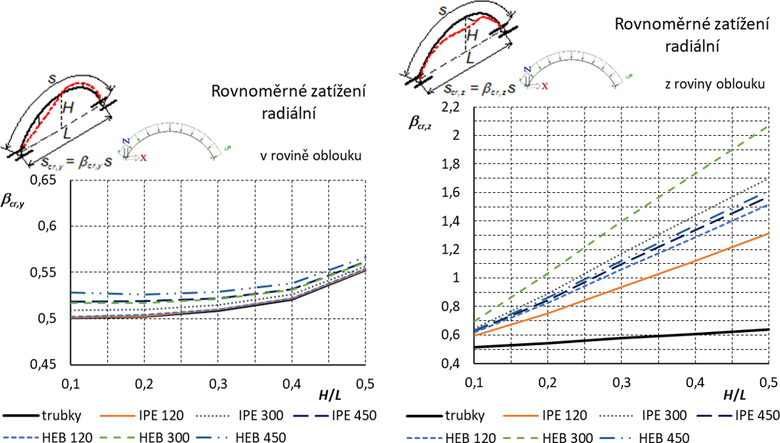
Obr. 9 Dvojkloubový oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
5. Vzpěrné délky vetknutých oblouků
(vztažené k osové síle v patě Nmax)
5.1 Zatížení po délce oblouku
5.1.1 Trubky a otevřené průřezy „na stojato“
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 10. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δD1) a z roviny oblouku (δD2) uvedeny v Tab. 4. Hodnota Nmin pro δD1 je stanovena v s/6 a pro δD2 v s/4.
Obr. 10 Příklad vetknutého oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δD1 | 0,991 | 0,973 | 0,955 | 0,941 | 0,930 |
| √δD2 | 0,987 | 0,960 | 0,932 | 0,910 | 0,893 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 11.
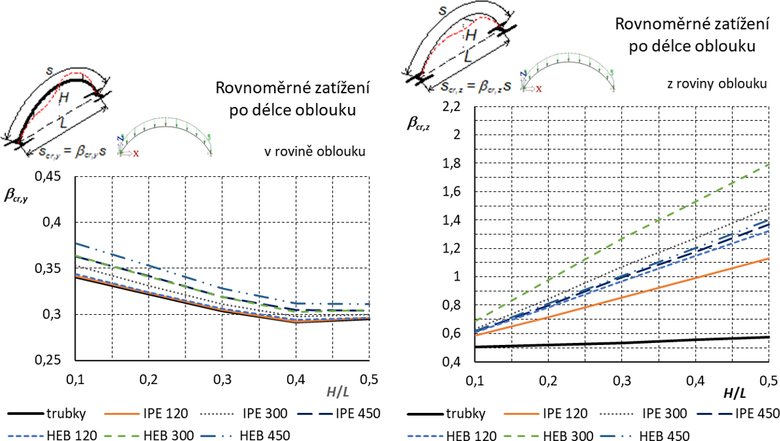
Obr. 11 Vetknutý oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
5.1.2 Trubky a otevřené průřezy „na ležato“
Pro vetknuté oblouky platí stejné závislosti jako u dvojkloubových oblouků s vidlicovým uložením a vliv poměru momentu setrvačnosti k momentu v prostém kroucení (Iz /IT) je pro vybočení oblouku z roviny rozhodující. Studie pro oblouky s průřezem „na ležato“ a rovnoměrným zatížením po délce oblouku je uvedena na obr. 12. Je opět zřejmé, že součinitele pro vybočení v rovině oblouku nyní splývají se součiniteli pro trubky, pro vybočení z roviny jsou však ve srovnání se součiniteli vzpěrných délek pro průřezy orientovanými „na stojato“ mnohem vyšší. Pro další typy zatížení vetknutých oblouků je situace opět obdobná a poloha „na ležato“ není uváděna.
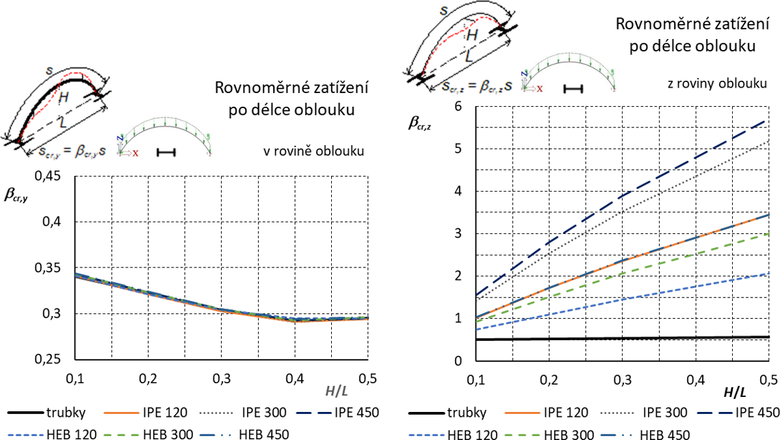
Obr. 12 Vetknutý oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na ležato“
5.2 Zatížení na půdorys oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 13. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δD1) a z roviny oblouku (δD2) uvedeny v Tab. 5. Hodnota Nmin pro δD1 je stanovena v s/6 a pro δD2 v s/4.
Obr. 13 Příklad vetknutého oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δD1 | 0,992 | 0,976 | 0,962 | 0,952 | 0,944 |
| √δD2 | 0,987 | 0,963 | 0,943 | 0,928 | 0,914 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 14.
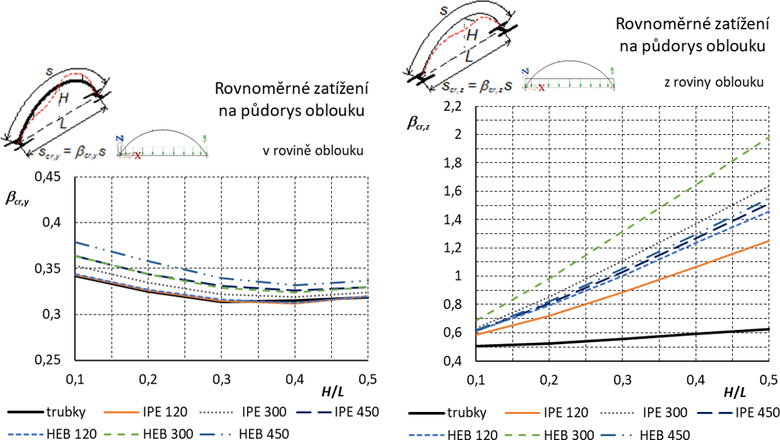
Obr. 14 Vetknutý oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
5.3 Radiální zatížení oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 15. Protože osová síla v oblouku je konstantní, pro převodní součinitele platí δT = δD = 1.
Obr. 15 Příklad vetknutého oblouku s poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 16.
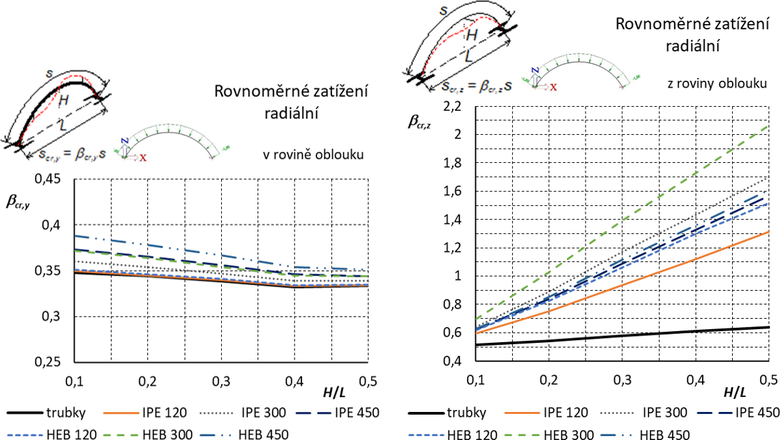
Obr. 16 Vetknutý oblouk: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku Otevřené průřezy jsou orientovány „na stojato“
6. Závěr 1. části
Uvedené křivky součinitelů vzpěrných délek dvojkloubových oblouků s vidlicovým uložením a oblouků vetknutých jsou vztaženy k osové síle v patě oblouků (Nmax) a vedou k následujícím závěrům:
- Vliv tvaru průřezu (uzavřené trubky, otevřené IPE a HEB) je pro součinitele vzpěrných délek v rovině oblouku výraznější pro ploché oblouky, a naopak pro vzpěrné délky z roviny oblouku se více odlišuje u vysokých oblouků a je podstatný. Z analýzy křivek vzpěrných délek a Tab. 1 plyne, že rozhodujícím parametrem pro vybočení z roviny oblouků je poměr tuhosti k ose pro vybočení z roviny oblouku a tuhosti v prostém kroucení (Iz /IT). Výrazně vyšší hodnoty součinitelů vzpěrných délek pro vybočení z roviny oblouků jsou proto u průřezů orientovaných „na ležato“, kde je uvedený poměr vysoký. U profilů IPE a HEB orientovaných „na stojato“ lze provádět interpolaci hodnot pod a nad hraničními průřezy IPE300 a HEB300.
- Vliv tvaru zatížení (rovnoměrné na délku oblouku, rovnoměrné na půdorys oblouku, rovnoměrné radiální) na součinitele vzpěrných délek v rovině i z roviny oblouku je výraznější pro vysoké oblouky, naopak pro ploché oblouky je nevýrazný. Součinitele vzpěrných délek pro zatížení nerovnoměrná, popř. lokální, nebyla řešena.
- Součinitele vzpěrné délky pro vybočení z roviny se u dvojkloubových oblouků s vidlicovým uložením a vetknutých oblouků pro stejná zatížení (rovnoměrné na délku oblouku, rovnoměrné na půdorys oblouku, rovnoměrné radiální) téměř neliší.
- Součinitele vzpěrných délek jsou lineárně závislé na vztažné délce, v této studii je jí délka oblouku s. Pro jiné vztažné délky (např. s/2 nebo L, jak je tomu např. v Eurokódu ČSN EN 1993-2) lze tedy provést jednoduché přenásobení poměrem vztažných délek. V této souvislosti lze upozornit, že hodnoty vzpěrných délek v běžných normách (a též v ČSN EN 1993-2) platí pouze pro uzavřené průřezy (trubky) a nezahrnují korekci na vliv proměnné síly v oblouku. Ze studie rovněž plyne, že kritické tvary vybočení pro případné řešení geometricky nelineární analýzou (GNIA), popř. zjednodušenou teorií 2. řádu, jsou závislé na okrajových podmínkách. Pro vetknuté oblouky a vybočení v rovině oblouku, popř. běžné vidlicové uložení dvojkloubových oblouků pro vybočení z roviny oblouku, není tvar vybočení z vetknutí v normách předpokládán.
7. Literatura
- [Macháček, J.: Stabilita ocelových kruhových oblouků, TZB-info, ocelové konstrukce, 8. 3. 2021, 12 s.,
https://stavba.tzb-info.cz/ocelove-konstrukce/21953-stabilita-ocelovych-kruhovych-oblouku
Poděkování
Článek a související výzkum vznikl za podpory grantu ČVUT SGS22/141/OHK1/3T/11.
Results of extensive study concerning buckling lengths of circular steel arches are presented. The study in Part 1 covers two-hinged and built-in arches, in Part 2 three-hinged arches with the crown hinge of a fork type (in the arch plane only) and a full type (both in and out of the arch plane). All studies present three uniform loading patterns (vertical along the arch length, vertical to the arch plan or radial to the arch axis). Buckling lengths of the equivalent straight (Euler’s) column with the constant axial force corresponding to maximal axial arch force in the arch bases are presented in the form of graphs for CHS (circular hollow sections) and various open rolled IPE and HEB cross-sections. The study is a follow-up of the author’s article Stability of Steel Circular Arches [1], embodying the preliminary stability analysis of two-hinged arches.