Pokročilé modely styčníků a globální analýza ocelových konstrukcí
Globální analýza prutových ocelových stavebních konstrukcí se při projektování řeší prostorovým prutovým modelem. Připojení prutů ke styčníkům se předpokládá dokonale tuhé nebo se modeluje pomocí volných, případně pružných kloubů. Nová metoda CBFEM umožňuje modelovat styčník podrobně. Lze získat tuhost, únosnost a deformační kapacitu přípojů jednotlivých prutů, které jsou v něm spojeny. CBFEM model je třeba zatížit odpovídajícími vnitřními silami, které byly získány při globální analýze. Článek vysvětluje problematiku zatěžování podrobného prostorového modelu a poukazuje na situace, kdy skutečné konstrukční řešení styčníku neodpovídá teoretickým předpokladům globálního modelu.
CBFEM – nová úroveň analýzy ocelových styčníků a přípojů
Metoda konečných prvků (MKP, FEM) je obecná metoda běžně používaná pro statickou analýzu konstrukcí. Již od osmdesátých let se objevovaly pokusy použít MKP pro vědecké modely styčníků [1]. Pro analýzu je nezbytné použít pružně-plastický materiál. Nicméně výsledky MKP jsou bezcenné bez důkladné validace modelů experimenty.
Pro použití v inženýrské praxi byl vyvinut model, který využívá MKP pro určení vnitřních sil a napětí ve styčníku a metody komponent pro posouzení spojovacích prvků – Component based finite element method (CBFEM) [2]. Materiál je pro návrhové účely modelován jako ideálně plastický [3].
Stěny i pásnice připojených prutů jsou v CBFEM modelovány jako stěno-desky, pro které existuje známé a ověřené řešení. Spojovací prvky – šrouby a svary – jsou nejsložitější částí výpočetního modelu. Jejich modelování v obecných MKP programech je velmi složité kvůli pracnosti i proto, že uživatel v okamžiku návrhu nezná potřebné vstupní údaje. Proto je lepší vyvinout speciální prvky pro modelování šroubů a svarů.
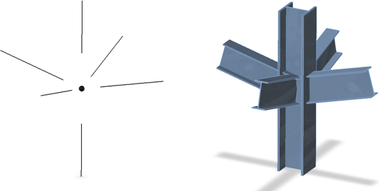
Při globální analýze ocelových rámů nebo příhradových konstrukcí jsou styčníky uvažovány jako nehmotné body. V nich se sestavují rovnice rovnováhy a po jejich vyřešení jsou dopočteny vnitřní síly na koncích všech prutů. Styčník je zatížen koncovými vnitřními silami připojených prutů. Jejich výslednice je nulová, neboť styčník musí být v rovnováze. Při této analýze není znám skutečný tvar styčníku. Inženýr jen rozhoduje, jestli je připojení jednotlivých prutů tuhé nebo kloubové.
Obrázek 1 – Teoretický (nehmotný) styčník a skutečný tvar bez koncových úprav prutů
Pro důvěryhodný návrh styčníku je nutné respektovat skutečný stav, jak je styčník navržen v konstrukci.
Koncové síly na prutech jsou pro přesnější CBFEM model aplikovány jako zatížení na koncích jednotlivých prutů. Šestice sil z teoretického styčníku je přenesena na konec segmentu – velikosti sil zůstávají stejné, ale momenty jsou upraveny o účinky sil na příslušných ramenech [4].
Konce segmentů na straně styčníku nejsou propojeny. Propojení je nutné vykonstruovat. K tomu v CBFEM metodě slouží tzv. výrobní operace. Jsou to zejména: ořezy, odtahy, otvory, výztuhy, žebra, čelní a příložné desky, úhelníky, styčníkové plechy a řada dalších. Ty jsou doplněny o spojovací prostředky – svary a šrouby.
Ocelové desky
Obrázek 2 – Modely pracovního diagramu
Všechny části prutových prvků a všechny přídavné plechy jsou modelovány jako stěno-desky. Jejich materiálem je ocel (obecně kov) a ta se chová výrazně nelineárně. Nelinearitu (plasticitu) je potřeba ve výpočtu zohlednit.
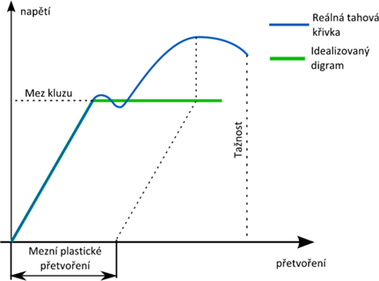
Ve stavební praxi se skutečný pracovní diagram oceli nahrazuje pro potřeby návrhu ideálně plastickým materiálem, viz obr. 2. Výhodou ideálně plastického materiálu je, že stačí znát mez kluzu a modul pružnosti pro popis pracovního diagramu. Stavební oceli mají zaručenou tažnost 15 %. Pro běžné navrhování lze použít reálnou mezní hodnotu plastického přetvoření 5 % (1993-1-5 příloha C odstavec C.8, poznámka 1).
Při použití ideálního pružně-plastického pracovního diagramu nemohou napětí v oceli překročit mez kluzu. Posudek napětí tedy nemá smysl provádět. Jako posudková veličina je vhodnější poměrné plastické přetvoření [5].
Svary
Ocelové desky působí ve styčníku jako samostatné prvky. Jejich propojení zajišťují svary a šrouby.
CBFEM metoda se snaží maximálně kopírovat skutečný stav. Výpočtové stěno-desky nejsou propojeny, neřeší se žádné jejich proniky, tak jak se to běžně dělá při modelování budov a konstrukcí. Síť konečných prvků se vytváří samostatně na každé desce nezávisle na sítích ostatních desek.
Svary jsou modelovány jako speciální nehmotné silové interpolační vazby, které zajišťují propojení hrany jedné desky s plochou nebo hranou desky druhé.
Obrázek 3 – Pracovní diagram šroubu v tahu
Šrouby
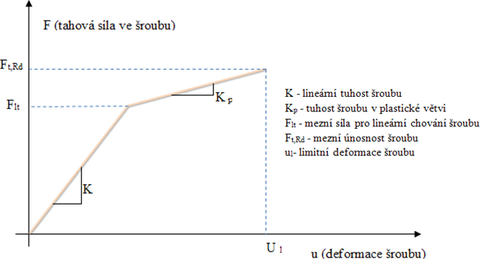
Kotevní šrouby (a šrouby obecně) se v CBFEM modelují jako jednoduché pružiny s různými pracovními diagramy pro tah a smyk. Při osovém namáhání působí šroub pouze v tahu, tlaková síla v něm nemůže vzniknout. Při smykovém namáhání působí pružina symetricky na obě strany. Koncové body šroubu/pružiny opět nejsou přímo zapojeny do sítě konečných prvků na plechu. Pro spojení jsou použity silové interpolační vazby.
Rovnováha ve styčníku
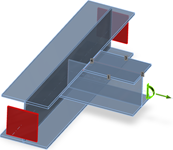
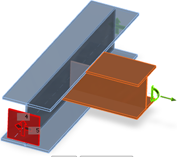Obrázek 4 – Zjednodušený a přesný model podepření CBFEM modelu styčníkuKaždý styčník ve 3D MKP modelu musí být v rovnováze. Požadavek rovnováhy je naprosto správný, ale zvláště pro návrh jednodušších styčníků není nutný vysvětlit. Ve styčníku je vždy jeden prvek „nosný“ a ostatní jsou k němu připojené. Pokud nás zajímá jen připojení nesených prvků, rovnováhu není nutné řešit. Lze použít dva režimy zadání zatížení – viz obr. 4
Zatížení modelu styčníku
Koncové síly prutu z rámového modelu se přenášejí na konce prutových segmentů. Při tom se zohlední i excentricity prutů, které vzniknou v důsledku konstruování styčníku.
CBFEM metoda vytváří výpočetní model co nejvěrněji podle skutečného stavu. Naopak výpočet vnitřních sil se provádí na velmi zidealizovaném 3D MKP prutovém modelu, ve kterém jsou jednotlivé prutové prvky modelovány střednicemi a styčníky nehmotnými uzly.
a) Skutečný tvar styčníku
b) Teoretický tvar v 3D MKP modelu
Obrázek 5 – Přípoj vodorovného nosníku ke svislému sloupu
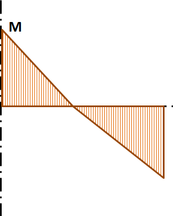
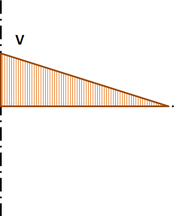
Vnitřní síly se počítají na 3D prutovém modelu. Na obrázku 6 je příklad možného průběhu vnitřních sil na vodorovném nosníku.
a) Ohybový moment
b) Posouvající síla
Obrázek 6 – Průběh vnitřních sil na vodorovném nosníku. M a V jsou koncové síly ve styčníku.
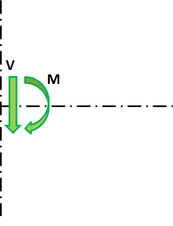
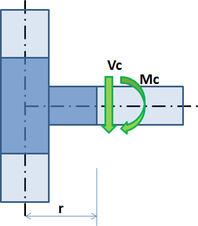
Pro potřeby navržení styčníku (přípoje) jsou důležité účinky prutu na styčník. Ty jsou znázorněny na obrázku 7.
a) 1D prutový model
b ) CBFEM model – tmavě modrá barva
Obrázek 7 – Zatěžovací účinky prutu na styčník. CBFEM model je nakreslen tmavě modře.
Obrázek 8 – Průběh ohybového momentu na CBFEM modelu. Šipka ukazuje skutečnou pozici přípoje.
V teoretickém styčníku působí moment MEd a síla VEd. Model je potřeba zatížit příslušnými účinky M a V, které je nutné přenést na konec segmentu do vzdálenosti r.
VEd,c = VEd
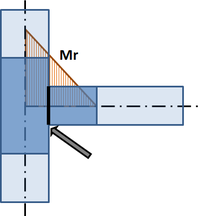
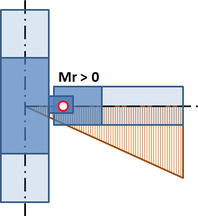
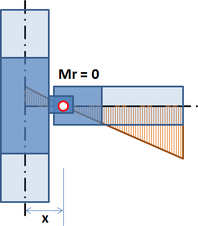
Pro návrh přípoje je nutné si uvědomit, kde se skutečně nachází a v jaké pozici je vůči teoretickému styčníku. V místě skutečného přípoje jsou zpravidla jiné vnitřní síly než v teoretickém styčníku. Díky přesnému modelu CBFEM lze návrh převézt na redukované síly – viz moment MEd,r na obrázku 8.
Při zatěžování styčníku je důležité, že řešení skutečného styčníku musí odpovídat teoretickému modelu, na kterém byly počítány vnitřní síly. To spolehlivě platí u tuhých styčníků, ale u kloubů může být situace zcela jiná.
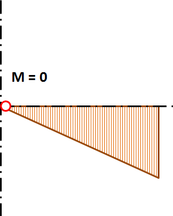
Na obrázku 9 je znázorněno, že poloha kloubu v teoretickém prutovém modelu se liší od polohy v reálné konstrukci. Teoretický model tudíž neodpovídá skutečnosti. Při použití vypočítaných koncových sil je do odsunutého přípoje aplikován výrazný ohybový moment a styčník vyjde předimenzovaný nebo nelze navrhnout vůbec. Řešení je prosté – je nutné sladit oba modely. Buď zadat kloub v prutovém modelu do přesné polohy, nebo posunout křivky vnitřních sil tak, aby nulový moment byl skutečně v místě kloubu (obr. 10).
a) 1D prutový model
b ) CBFEM model – tmavě modrá barva
Obrázek 9 – Pozice kloubu na teoretickém 3D FMKP prutovém modelu a na skutečné konstrukci
Obrázek 10 – Posunutá křivka ohybového momentu na nosníku. Nulový moment je v místě kloubu.
Modelování styčníků při celkové 3D analýze
Celkové chování konstrukce je ovlivněno chováním styčníků. Proto je důležité co nejpřesnější modelování styčníků. Pro zajištění kvality celkových modelů konstrukcí zavádí ČSN EN 1993-1-8 ) [6] v kapitole 5 klasifikaci styčníků založenou na relativní tuhosti připojeného prvku. Přípoj může být klasifikován jako tuhý, kloubový nebo polotuhý podle rotační tuhosti srovnáním počáteční tuhosti Sj,ini s klasifikačními mezemi. Přípoj může být klasifikován na základě provedených testů, na základě zkušeností s předchozími příklady nebo výpočtem. V případě polotuhých styčníků nabízí kapitola 5.3 v EN 1993-1-8 zjednodušenou transformaci tuhosti stěny sloupu ve smyku do rotační tuhosti přípoje.
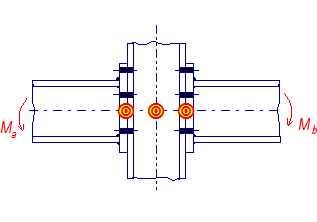
a) Skutečný model styčníku s oboustrannými přípoji
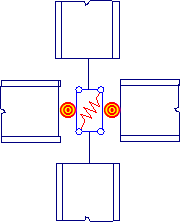
b) Model styčníku se stěnou ve smyku a dvěma pružinami představující přípoje
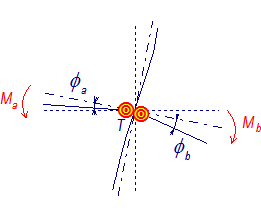
c) Zjednodušení ve 3D modelu
Obrázek 11 – Model polotuhého styčníku v celkové analýze konstrukce
CBFEM je nástroj pro každodenní praxi
CBFEM metoda je synergií standardní komponentní metody a pokročilé MKP analýzy. Inženýři-statici tak dostávají výkonný, rychlý a přesný nástroj pro analýzu ocelových styčníků. Ocelové styčníky a přípoje, které se musely dříve jen zjednodušovat nebo odhadovat, lze nyní analyzovat přesně.
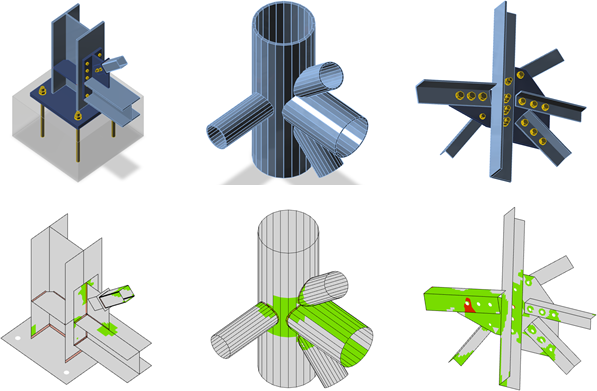
Obrázek 12 – Příklady složitých styčníků vyřešených metodou CBFEM
Reference
- Virdi KS et al, 1999, Numerical simulation of semi-rigid connections by the finite element method, Report of Working Group 6, Numerical Simulation COST C1, Brussels Luxembourg.
- Wald, F., et al. Benchmark cases for advanced design of structural steel connections. Praha: Česká technika – nakladatelství ČVUT. 2016, ISBN 978-80-01-05826-8.
- Heinisuo M., Laine V., Lehtimäki E. 2009. Enlargement of the component method into 3D, Proceeding of Eleventh Nordic Steel Construction Conference, NSCC2009.
- Šabatka L., Wald F., Kabeláč J., Kolaja D., Vnitřní síly působící na styčník a globální analýza ocelových konstrukcí, Konstrukce, 3/2016, 54–57.
- ČSN EN 1993-1-5, Navrhování ocelových konstrukcí, Boulení stěn, ČNI, Praha, 2006.
- ČSN EN 1993-1-8, Navrhování ocelových konstrukcí, Navrhování styčníků, ČNI, Praha, 2006.
Steel frame structures are commonly analyzed three dimensionally by 1D elements. Connection of elements to joints is assumed to be perfectly rigid, nominally pinned or semi-rigid. The new CBFEM method allows to properly model the connection. The bending/deformation stiffness, resistance and deformation capacity of connections of individual members is evaluated. CBFEM model is loaded with appropriate internal forces obtained by global analysis. The article explains loading of a detailed 3D model of a joint. It also addresses situation where actual structural design of the joint does not match theoretical expectations of the global analysis.