Reklama

Výpočetní modely vaznicového krovu

3.6.2013

Ing. Josef Musílek, Ph.D., Ing. Jan Plachý, Ph.D., VŠTE České Budějovice

Recenzovaný

Článek se zabývá statickýcm návrhem vaznicového krovu, který je v současnosti často využíván, zejména při stavbě rodinných domů. Jsou ukázány různé výpočetní modely vaznicového krovu a je provedeno jejich porovnání a zhodnocení.

Reklama

Úvod

V současné době projektanti a statici bežně používájí pro návrh a statické posouzení stavebních konstrukcí výpočetní programy. Tyto programy jsou založeny na principu konečných prvků a jsou používány zejména pro výpočet vnitřních sil na konstrukcích. Celá řada programů dnes umí také jednotlivé konstrukční prvky staticky posoudit podle příslušných návrhových norem.

Při statickém návrhu a posouzení stavební konstrukce, i když je proveden za pomocí statického výpočetního softwaru, je nejobtížnější na začátku stanovit správný statický model konstrukce a statické působení nosného systému. Přesný výpočetní model, který by vystihoval skutečné chování konstrukce, není možné v běžné praxi obvykle stanovit. Statik musí tedy nalézt idealizovaný výpočetní model, který co nejlépe vystihuje chování skutečné konstrukce. U určitých typů konstrukce není nalezení idealizovaného výpočetního modelu velkým problémem, zejména pokud se jedná u staticky určitou konstrukci. U krovů, které jsou téměř vždy staticky neurčité, je však častým problémem určit tento idealizovaný výpočetní model, zejména co se týká vodorovnéhoi podepření krovu, proti vodorovnému posuvu.

V následujícím textu je uveden konkrétní příklad jednoduchého vaznicového krovu se středovými vaznicemi. Jsou prezentovány různé výpočetní modely tohoto krovu, které se liší různým vodorovným podepřením v místě pozednic a vaznic. V příspěvku jsou uvedeny výsledky jednotlivývh modelů - konkrétně průběhy ohybových momentů, průběh normálových sil, velikost svislých a vodororovných sil do pozednic a vaznic. Na závěr je provedeno shrnutí výsledků z jednotlivých modelů a je zhodnocena vhodnost a výstižnost každého výpočetního modelu. Výpočet byl proveden pomocí výpočetního software Scia Engineer.

Zadání vaznicového krovu

Na Obr. 1 je znázorněna vazba krovu, pro kterou byly porovnány jednotlivé výpočetní modely. Střecha je dlouhá 12,48m (délka měrená ve směru hřebene) a široká 10,20m (délka měřená kolmo na hřeben). Jednotlivé vazby krovu jsou od sebe vzdálené 1m a všechny jsou opatřeny kleštinami. Vaznice jsou uloženy na příčných nosných zdech.

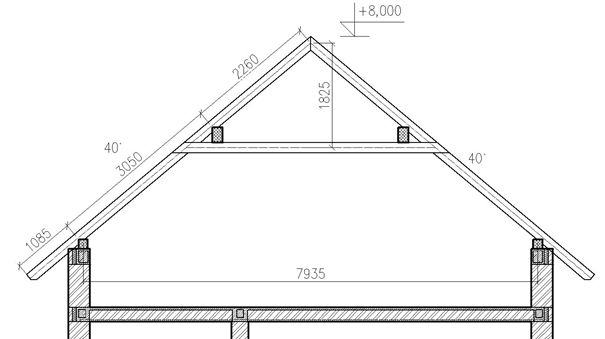
Obr. 1 Vazba krovu – řez

Jedná se o krov rodinného domu s obytným podkrovím. Střecha je poktyta pálenými taškami. V oblasti krokve mezi vaznicí a pozednicí a na kleštinách, se nachází podhled, který je proveden ze sádrokartonovývh desek. V této oblasti je také provedena teplená izolace. Užitné zatížení na kleštinách se neuvažuje.

Vstupní údaje pro výpočet klimatických zatížení:
Sněhová oblast III.
Větrová oblast: II.

Zatížení krovu je spočítáno v souladu se soustavou Evropských norem pro zatížení. Ve výpočtu je uvažováno se stálým zatížením od vlastní hmotnosti krovu a od skladby střechy, se zatížením od sněhu a s příčným zatížením od větru, jehož působení se předpokládá z prava doleva, jak je vyznačeno šipkou na Obr. 1. Při výpočtu jsou uváženy dvě kombinace, ve kterých se kombinují výše uvedená zatížení (stálé+sníh+vítr)

Uvažované kombinace:
MSÚ 1: 1,35 x stálé + 1,5 x sníh + 0,9 x příčný vítr
MSÚ2: 1,35 x stálé + 0,75 x sníh + 1,5 x příčný vítr

Výpočetní model krovu č.1

V tomto výpočetním modelu je proti vodorovnému posunu podepřena pozednice, která je na návětrné straně střechy. Ostatní podpory (vaznice a pozednice na závětrné straně) jsou vodorovně posuvné. Tento model odpovídá situaci, kdy vaznice nejsou na vnitřních příčných zdech příčně uchycené a jsou pouze podložené. Toto je častá praxe, kterou je možné vidět na řadě staveb. Vodorovné síly pak musí přenášet pozednice a pozednicový věnec. V tomto modelu je uvažováno, že vodorovnou sílu od větru přebírá pravý pozednicový věnec. Na Obr. 2 a Obr. 3 jsou nakreslené průběhy ohybového momentu a normálové síly na prvcích krovu.

Obr. 2 Průběh ohybového momentu M_y [kNm] pro kombinaci MSÚ 1

Obr. 3 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Výpočetní model krovu č.2

Tento výpočetní model předpokládá, že vodorovnou sílu přebírá oproti modelu č. 1 levá pozednice na závětrné straně střechy.

Obr. 4 Průběh ohybového momentu M_y [kNm] pro kombinaci MSÚ 1

Obr. 5 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Výpočetní model krovu č.3

Tento výpočetní model předpokládá, že obě pozednice jsou vodorovně podepřeny a podílejí se tedy obě na přenosu vodorovné síly od větru. Tento model však neposkytuje dobré výsledky z hlediska statického působení krovu při svislém zatížení. Vlivem vodorovných neposuvných podpor v místě pozednic, vznikají od svislého zatížení krovu velké boční síly do pozednic. Statické chování tohoto modelu se blíží chování hambálkového krovu. Těmto vodorovným bočním silám v místě pozednic vzdoruje jen běžné osedlání krokví na pozednici doplněné běžným krovovým hřebíkem. Tento spoj není schopen takto velkou boční sílu přenést a dojde k vzájemnému posunutí krokve po pozednici v místě osedlání. Tím dojde ke změně statického působení krovu, kdy se jedna podpora v místě pozednice stává posuvnou a získáváme tak v podstatě model č. 1 nebo 2.

Obr. 6 Průběh ohybového momentu M_y [kNm] pro kombinaci MSÚ 1

Obr. 7 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Výpočetní model krovu č.4

V tomto modelu uvažujeme, že spoj krov-pozednice a provedení pozedního věnce s nadezdívkou nejsou schopny přenášet vodorovné síly od větru. Jediným prvkem, který je tedy možné použít na přenos vodorovných sil od příčného větru jsou vaznice. V tomto modelu uvažujeme, že vodorovné síly od příčného větru přenáší pravá vaznice na návětrné straně střechy. Pokud v modelu předpokládáme, že vodorovné síly přenáší vaznice, pak tyto vaznice musí být na nosných příčných zdech řádně ukotveny proti příčnému posunu. Dále je také třeba uvážit vodorovné zatížení vaznic při jejich dimenzování.

Obr. 8 Průběh ohybového momentu My [kNm] pro kombinaci MSÚ 1

Obr. 9 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Výpočetní model krovu č.5

Tento model je podobný jako model č.4, pouze se předpokládá, že vodorovnou sílu od větru přenáší levá vaznice na závětrné straně.

Obr. 10 Průběh ohybového momentu M_y [kNm] pro kombinaci MSÚ 1

Obr. 11 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Výpočetní model krovu č.6

Tento model předpokládá, že se v místě obou vaznic nachází vodorovně neposuvná podpora. Tento předpoklad není u běžného vaznicového krovu obvykle splněn. Podobně jako u pozednice, je krokev na vaznici osedlána běžným způsobem a osedlání je zajištěno běžným krovovým hřebíkem. Dále jsou vzanice ve vodorovném směru poddajné, zejména v blízkosti středu rozpětí vaznice, takže také z tohoto důvodu nelze předpokládat tuhou boční podporu. Výše uvedené důvody způsobí vodorovný posun vaznic směrem od sebe, aktivaci kleštin na tah a v podstatě přechod na model č. 4 popř 5.

Obr. 12 Průběh ohybového momentu M_y [kNm] pro kombinaci MSÚ 1

Obr. 13 Průběh normálové síly N[kN] pro kombinaci MSÚ 1

Číselné výsledky pro výpočetní model č. 1

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 1,3 kNm
Maximální moment na krokvi nad vaznicí (pro kombinaci MSÚ 1): -2,06 kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): 1,8 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	4,66	8,15	10	4,71
Vodorovná reakce	0	0	0	2,05
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	3,17	6,36	9,43	3,24
Vodorovná reakce	0	0	0	3,41

Číselné výsledky pro výpočetní model č. 2

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 1,13 kNm
Maximální moment na krokvi nad vaznicí (pro kombinaci MSÚ 1): -1,74 kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): -0,03 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	6,23	6,59	8,43	6,27
Vodorovná reakce	2,05	0	0	0
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	5,77	3,75	6,83	5,84
Vodorovná reakce	3,41	0	0	0

Číselné výsledky pro výpočetní model č. 3

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 0,72 kNm
Maximální moment na krokvi nad vaznicí (pro kombinaci MSÚ 1): - 0,98 kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): -3,31 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	9,04	2,86	4,71	9,08
Vodorovná reakce	5,84	0	0	-3,80
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	7,25	1,36	4,44	7,32
Vodorovná reakce	5,46	0	0	-2,05

Číselné výsledky pro výpočetní model č. 4

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 1,3 kNm
Maximální moment na krokvi nad vaznicí (pro kombinaci MSÚ 1): - 2,06kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): -3,31 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	4,66	8,15	8,28	6,42
Vodorovná reakce	0	0	2,05	0
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	3,17	6,35	6,58	6,10
Vodorovná reakce	0	0	3,41	0

Číselné výsledky pro výpočetní model č. 5

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 1,13 kNm
Maximální moment na krokvi nad vaznicí (pro kombinaci MSÚ 1): - 1,74 kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): -0,08 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	4,51	8,30	8,43	6,27
Vodorovná reakce	0	2,05	0	0
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	2,91	6,61	6,83	5,85
Vodorovná reakce	0	3,41	0	0

Číselné výsledky pro výpočetní model č. 6

Maximální moment na krokvi v poli (pro kombinaci MSÚ1): 0,68 kNm
Maximální moment na krokvi nad pozdnicí (pro kombinaci MSÚ 1): - 1,02 kNm
Normálová síla v kleštině (pro kombinaci MSÚ 1): -4,89 kN

Reakce:

Reakce pro kombinaci zatížení MSÚ 1	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	4,10	8,71	8,84	5,86
Vodorovná reakce	0	7,50	-5,45	0
Reakce pro kombinaci zatížení MSÚ 2	Pozednice-Levá	Vaznice-Levá	Vaznice-Pravá	Pozednice-Pravá
Svislá reakce	2,64	6,88	7,10	5,58
Vodorovná reakce	0	6,98	-3,71	0

Porovnání získaných výsledků a zhodnocení modelů

Jak bylo řečeno a zdůvodněno v předchozím textu, modely č. 3 a 6 jsou pro běžný vaznicový krov nevhodné a nevystihují skutečné působení běžného vaznicového krovu.

Model č. 3 se chová částečně jako hambálkový krov, kde je velikost vodorovných sil do pozednic zmenšována svislým podepřením krokví v místě vaznic. Problém spočívá ve vzájemném poměru svislé poddajnosti vaznice a vodorovné poddajnosti pozedního věnce v místě vazby krovu. Například vazba, která se nachází uprostřed rozpětí vaznic, ve skutečnosti vyvolá větší vodorovné síly na pozednici a menší svislé síly do vaznice, než které vyšly z uvedeného výpočetního modelu. Tato vazba uprostřed rozpětí vaznic se pak bude ve skutečnosti chovat více jako hambálková. Naopak v blízkosti podpory vaznice se vazba bude chovat více jako vaznicová, protože svislá poddajnost vaznice v blízkosti podpory je malá. Od tohoto se také odvíjí veškeré vnitřní síly na prvcích. Je vidět že modely 3 a 6 dávají nejmenší velikosti ohybovývch momentů na krokev. Tyto ohybové momenty se však díky výše popsaným poddajnostem mohou zvýšit. Výsledky z uvedeného modelu jsou tak na straně nebezpečné.

Model č. 6 by šlo použít pouze v případě, že by bylo zabráněno vodorovnému posunu vaznic u každé vazby. To je možné dosáhnout řádným ukotvením vaznic na příčných zdech a vytvoření tuhé vodorovné podpory v místě vaznic. Toho lze docílit například vytvořením vodorovného vysokého nosníku, jehož horní a spodní okraj budou tvořit vaznice. Tento vodorovný nosník lze vytvořit například pomocí záklopu z OSB desek, který bude propojen s vaznicemi. Záklop z OSB desek tak bude tvořit stojinu a vaznice pásy vodorovného nosníku. Dále je možné také vytvořit vodorovný příhradový vazník, u kterého budou vaznice horním a dolním pasem, tím že se do prostoru mezi vaznicemi doplní diagonály. Je ale zřejmé, že toto řešení je pro běžný vaznicový krov zbytečné.

Ostatní výpočetní modely (1,2,4,5) jsou z hlediska maximálního ohybového momentu na krokvi prakticky shodné. Ohybový moment na krokvi má hlavní vliv na vlastní dimenzi průřezu.

Pro dimenzování vaznic je potřebná svislá a případně vodorovná reakce z podpory umístěné v místě vaznice. Velikost svislé síly do vaznice vychází maximální pro model č.1. Je cca o 15-20% vyšší než u modelů 2,4,5.

Vodorovná síla od příčného větru vychází u modelů 1,2,4,5 stejně a působí vždy tam, kde je zavedena pevná vodorovná podpora.

Provedení krovu v souladu s modelem č. 4 a 5 (tedy tak, že jsou vaznice v místě svých podpor na stěnách příčně drženy), není běžné. Vaznice bývají často pouze jen podloženy ve svislém směru, takže uložení vaznic není schopno přenášet vodorovné příčné síly. Navíc, často jsou vaznice podepřeny pouze sloupkem v prostoru, který nemůže vaznici poskytnout pevnou příčnou vodorovnou podporu do strany. Dalším problémem je skutečnost, že pokud by se vaznice dimenzovaly na kombinaci působení svislé a vodorovné síly, vycházely by rozměry vaznic poměrně velké. Vzhledem k těmto kopmlikacím, je proto výhodnější přisoudit vodorovné síly od větru pozednímu věnci. Pozední věnec z nadezdívkou a příslušné spoje (krokev-pozednice a pozednice-pozední věnec) musí být proveden tak, aby tyto vodorovné síly od větru byl schopný přenést. V tomto ohledu se jeví jako výstižnější modely č. 1 a 2.

Z modelu č.1 vychází o něco větší svislá síla do vaznice než u modelu 2 (i když jen cca o 15%). Také ohybové momenty na krokvi jsou u modelu č. 1 o něco vyšší než u modelu č.2. Model č. 1 je tak mírně na straně bezpečné. Normálová síla v kleštinách vychází u modělu č. 1 tahová, což odpovídá správné funkci kleštin (tahové působení). Vzhledem k těmto skutčnostem se jeví model č. 1 jako nejvhodnější a nejvýstižnější.

Závěr

V rámci tohoto příspěvku bylo porovnáno několik výpočetních modelů vazeb vaznicového krovu, které byly zatížené kromě svislých zatížení, také větrem působícím v příčném směru. Jednotlivé modely se lišily různými vodorovnými podepřeními v místech vaznic a pozednic. Jako nejvýstižnější výpočetní model byl vybrán model, který je vodorovně podepřen v místě pozednice, která se nachází na návětrné straně sedlové střechy.

Literatura

[1] ČSN EN 1990 – Zásady navrhování konstrukcí
[2] ČSN EN 1991-1-1 – Zatížení konstrukcí – Část 1-1: Obecná zatížení – Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb
[3] ČSN EN 1991-1-3 – Zatížení konstrukcí – Část 1-3: Obecná zatížení – Zatížení sněhem
[4] ČSN EN 1991-1-1 – Zatížení konstrukcí – Část 1-1: Obecná zatížení – Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb
[5] ČSN EN 1991-1-4 – Zatížení konstrukcí – Část 1-4: Obecná zatížení – Zatížení větrem
[6] Jelínek, J.: Tesařské konstrukce. Volyně. VOŠ Volyně. 2002

English Synopsis

Computational models of purlin roofs

The article deals with static design of saddle roof frame with two middle purlins. This kind of bearing stucture is widely used for roofing of family houses. There are shown diferent computational models. These models are compared and evaluated.