Prehľad aktuálnych výpočtových metód krížom lepeného lamelového dreva na účinky pretlačenia
Táto publikácia porovnáva zjednodušené analytické metódy na výpočet odolnosti v pretlačením lokálne podopretej stropnej dosky z krížom lepeného lamelového dreva (CLT). Práca porovnáva zjednodušené modely podľa Mesteka a Mustera. Referenčný experiment bol prevzatý z Mestekovej dizertačnej práce. Porovnaním týchto analytických modelov sa ukázalo, že žiadny z analytických modelov nedokázal presne predpovedať porušenie vzorky, čo vedie k nehospodárnemu návrhu.
Úvod
Posledné roky vývoja konštrukcií z krížom lepených lamelových panelov (CLT) so sebou priniesli inovatívne riešenia stropných konštrukcií v tomto type výstavby, a to lokálne podopreté stropy. Takéto riešenie však uvádza donedávna nepreskúmané spôsoby namáhania jednotlivých lamiel v nadpodperovej oblasti. Od roku 2010 bolo vydaných niekoľko publikácií, ktoré sa venujú rôznym podoblastiam danej problematiky, ako napríklad zjednodušené výpočtové modely [1], [2], zosilnenie nadpodperovej oblasti pomocou celozávitových skrutiek [1], [3], [4], zosilnenie nadpodperovej oblasti pomocou zhrubnutia prierezu dosky nad podperou [5], alebo aj prognózy do budúcich možných riešení stropných konštrukcií pomocou na tupo lepených spojov CLT panelov [6] obr. 1. Prebiehajúci experiment vo viacerých fázach sa koná na Univerzite v Severnej britskej Kolumbií v spolupráci s Fast+Epp, cieľom experimentu je poskytnúť dáta pre návrhu tohto typu konštrukcií [7].
Jedna z významných realizácií so zmieneným konštrukčným systémom je Brock Commons Tall wood House, internát Univerzity Britskej Kolumbie v Kanade, postavený v roku 2016 (obr. 2), kde bol na overenie návrhu krížom lepeného lamelového dreva použité experimenty v skutočnej mierke.
V takomto konštrukčnom riešení dominuje šmyková odolnosť namiesto ohybovej odolnosti, priehybu a kmitania stropnej konštrukcie ako je to pri líniovo uložených stropných doskách. Podľa Mustera [2] zlyhanie vo valivom šmyku nie je ani duktilné ani krehké. Ak je lamela namáhaná valivým šmykom iba lokálne, nelineárne deformácie pred zlyhaním dovolia redistribúciu napätí na dovtedy nenamáhané lamely. Na obr. 3 je možné vidieť priečny rez porušenou vzorkou s Musterovho experimentu.
Analýza šmykového napätia
Analýzy šmykového napätia možno rozdeliť na 3 základné problematiky:
- Tok šmykových síl do podpery,
- Výpočet šmykového napätia,
- Výpočet odolnosti v pretlačení.
Ako k týmto dielčím problémom, komplexnej problematiky analýzy šmykového napätia, jednotlivé výpočtové modely pristupujú je opísané v nasledujúcich kapitolách.
Prvú zjednodušenú metódu na určenie stavu napätosti predložil Mestek [1] vo svojej dizertačnej práci v roku 2011. Vychádza z tzv. Shear Analogy Method (SAV), v preklade Metóda šmykovej analógie), ktorá je uvedená v prílohe D normy DIN 1052.
Ďalším skúmaným modelom bude analytický model podľa Mustera [2], ktorý ho taktiež predostrel vo svojej dizertačnej práci v 2020.
Oba výpočtové modely vychádzajú z predpokladu, že roznos síl od hrany podpery prebieha pod uhlom 35° a zároveň kritický šmykový obvod sa nachádza v priesečníku strednice CLT panela a priesečníku tejto diagonály (obr. 4).
Tok šmykových síl do podpery
Mestek vo svojej dizeračnej práci vychádza z metódy šmykovej analógie, na základe ktorej vytvoril prútový model. Prútový model tvorí raster prútov v dvoch smeroch X a Y každých 100 mm v dvoch úrovniach A a B. Tuhosti prútov sú vypočítané na základe prílohy D.3 normy DIN 1052. Model je zaťažovaný v strede silou F viď obrázok 5, distribúcia síl pre jednotlivé líca podpery je následne určená zo súčtu šmykových síl Viz,A a Viz,B. Na základe výsledkov tejto parametrickej štúdie sú vyhodnotené regresné krivky, ktoré popisujú distribúciu síl v hlavnom nosnom smere podľa vzťahu (1), ktorý je platný pre pomer hrúbky lamely v smere x ku smeru y rovný 1.
Podľa Mesteka je tok šmykových síl závislý takmer výlučne len na pomere hrúbky lamely v smere x a y, a zároveň na počte vrstiev panela.
Muster pri určení síl v líci podpery vychádza z kombinácie pásikovej metódy od Hillerborga [8] a teórie nosníkovej siete od Homberga [9]. Výpočtový model vyjadruje súčinitele βx (2) a βy, ktoré definujú podiel priečnej sily nad podperou v smere x a y lokálneho súradnicového systému.
Priečna sila v hlavnom nosnom smere sa vypočíta podľa (3). Vxz rozumej ako súčet priečnych síl v dvoch lícach podpery v smere x lokálneho súradnicového systému panela.
Pre stredový stĺp siete stĺpov s pravidelným rastrom lx na ly platí, že priečna sila v hlavnom nosnom smere v jednom z líc podpier je rovná polovici Vxz. Postup pre výpočet priečnych síl nad ostatnými stĺpmi je podrobne opísaný v [2].
Na Musterovom modeli je možné vidieť, že tok šmykových síl je závislý od ohybových tuhostí a rozponov v dvoch nosných smeroch. Tento výpočtový postup je použiteľný za predpokladu rovnomerného rastru stĺpov.
Výpočet šmykového napätia
Mestek vo svojej dizertačnej práci píše, že v prípade krížom lepeného lamelového dreva bez lepenia kratších hrán lamiel, napätie vo valivom šmyku možno opísať rovnicou (4), kde sa priečna sila Viz prenáša cez efektívnu šírku podpery bi,eff , po účinnej výške, ktorá je súčet hrúbky lamely v smere x a y, prenásobený súčiniteľom kr,i , tabuľka 1. Súčiniteľ kA,i platí iba pre stĺpy uložené na hrane stropného panela, kde tento súčiniteľ upravuje priemernú hodnotu napätia na efektívnej šírke bi,eff na maximálnu hodnotu šmykového napätia, z dôvodu nerovnomernej distribúcie šmykového napätia nad týmito stĺpmi. Hodnoty súčiniteľa kA,i sú uvedené v literatúre [1].
Model podľa Mustera hovorí o výpočte šmykového napätia na základe parabolického priebehu napätí na štvorcovom homogénnom priereze podľa vzorca (5), kde sila Fd je sila v podpere a tCLT je celková hrúbka CLT panela. Rovnica (5) je použiteľná iba v prípade ak pomer rozponov a pomer ohybových tuhostí je blízky 1. V iných prípadoch je potrebné rovnicu doplniť o súčinitele βx (2) a βy.
| Súčiniteľ kR,i | Počet lamiel | |||
|---|---|---|---|---|
| 5 | 7 | 9 | 11 | |
| kR,x | 2,00 | 2,50 | 3,33 | 3,89 |
| kR,y | 1,00 | 2,00 | 2,50 | 3,33 |
Pre šmykové napätie v ľubovoľnom líci podpery platí vzťah (5). Sila Viz je sila v líci podpery podľa Musterovho modelu distribúcie šmykových síl. Rovnica je doplnená o faktor kedge , ktorý zohľadňuje prítomnosť otvoru v CLT paneli priamo nad stĺpom a je bližšie opísaný v uvedenej literatúre [1]
Výpočet odolnosti v pretlačení
Podľa Mesteka 5percentný kvartil pevnosti reziva vo valivom šmyku je možné vynásobiť súčiniteľom kr,90 (6), (7), ktorý zohľadňuje zvýšenie pevnosti vo valivom šmyku vplyvom tlakového napätia kolmo na vlákna σc,90.
Podľa Mustera 5percentný kvartil pevnosti reziva vo valivom šmyku (8) je možné vynásobiť súčiniteľom kr,pu = 1,60, ak je krížom lepené lamelové drevo podrobené koncentrovanému zaťaženiu, ako to je v prípade bodovo podopretých stropných dosiek. Ak ide o krajný stĺp, kr,pu by mal byť obmedzený na 1,30.
Porovnanie výpočtových metód
Pre porovnanie zjednodušených metód bol vykonaný výpočet, ktorý porovnáva odolnosť CLT panela v pretlačení a šmykové napätie pri dosiahnutí zlyhania vzorky z experimentu podľa dizertačnej práce Mesteka [1], čo bude referenčnou hodnotou pri porovnaní. Prvou a druhou metódou M1 a M2 sa zaoberali predchádzajúce kapitoly. Výpočet je zároveň doplnený o ďalší výpočtový postup M3, ktorý rešpektuje Musterovu distribúciu síl ale šmykovú napätosť na efektívnom priereze počíta na základe Grashofovho vzorca (9). Poslednou metódou M4 je kombinácie metód M1 a M2, kde sa preberá distribúcia síl z Musterovho modelu M2 a výpočet šmykových napätí a odolností z modelu M1.
Porovnávané sú 4 výpočtové metódy:
- M1 – Model podľa Mesteka,
- M2 – Model podľa Mustera,
- M3 – Model podľa Mustera so šmykovým napätím podľa Grashofa,
- M4 – Model podľa Mustera so šmykovým napätím podľa Mesteka.
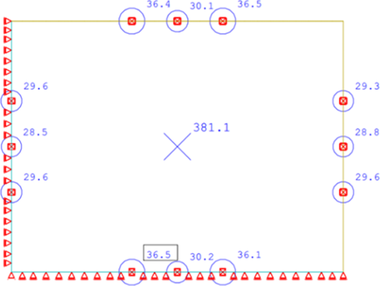
Porovnanie je vykonané na vzorke 5vrstvového CLT panela s hrúbkou lamiel 27 mm a celkovou hrúbkou 189 mm viď obr. 6. Rezivo panela má strednú hodnotu pevnosti vo valivom šmyku fRv,mean = 0,95 MPa. Panel má celkové rozmery 1,46 na 1,1 m (smer x na smer y), vzorka je podopretá po obvode a tlačená v strede lisom s čelnou platňou 300 na 300 mm. Celkovo boli porušené 3 vzorky, stredná hodnota porušenia Fmean = 381,12 kN viď obrázok 7. Vzorky sú zosilnené na účinky tlaku kolmo na vlákna aby nenastalo zlyhanie týmto spôsobom.
Bol zhotovený aj jednoduchý doskový model skúšky, pre overenie distribúcie síl do jednotlivých smerov. Výpočtový model je zhotovený v programe SOFiSTiK, doska je modelovaná za použitia funkcie vrstveného materiálu. Materiálové charakteristiky sú použité pre rezivo C24. Podpery sú tuhé kĺbové. Rozmery vzorky a polohy podpier boli určené na základe referenčného experimentu.
Ďalším predmetom porovnania sú hodnoty napätí vo valivom šmyku zjednodušenou metódou podľa Mesteka (4) a hodnôt podľa Grashofovho vzorca (9), od jednotkovej sily, pre rôzne konfigurácie prierezu CLT panela. Skúmané sú 5,7 a 9vrstvové panely pre pomery hrúbky lamiel 0,5, 0,75, 1,0, 1,33 a 2,0.
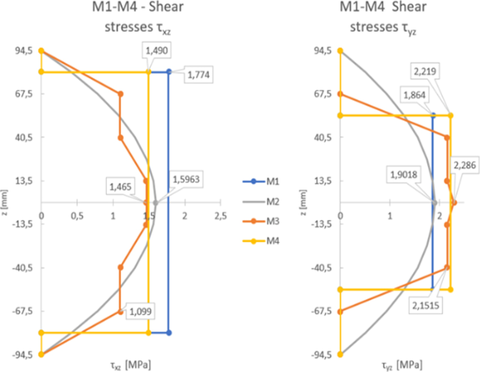
Tabuľka 3 sumarizuje výsledky jednotlivých metód, kde VRi je šmyková odolnosť príslušného smeru (súčet odolností pri dvoch lícach podpery), Vi je šmyková sila pre príslušné smery, pri zaťažení silou Fmean. Šmykové napätia τi sú napätia vo valivom šmyku vyvolané silou v príslušnom líci podpery na kritickej vrstve panela. Z výsledkov je zrejmé, že zlyhanie nastane vo vedľajšom nosnom smere skôr, čo sa zhoduje aj s priebehom experimentu. V zhrnutí je možné pozorovať významný rozdiel v šmykových sílách pre jednotlivé smery i. Dôvodom takéhoto rozdielu je, že metóda M1 vychádza výlučne z empirických meraní parametrickej štúdie vychádzajúcej z metódy SAV, na limitovanej vzorke s obmedzenými parametrami. Zatiaľ čo metódy M2 až M4 pri distribúcií šmykových síl zohľadňujú ohybové tuhosti a príslušné rozpony. Správnosť distribúcie síl podľa modelov M2 až M4 bola potvrdená jednoduchým doskovým MKP modelom podľa obr. 8.
| Výpočtový postup | Fmean [kN] | VRx [kN] | VRy [kN] | Vx [kN] | Vy [kN] | τx [Mpa] | τy [Mpa] |
|---|---|---|---|---|---|---|---|
| M1 | 381,12 | 244,94 | 233,10 | 207,06 | 174,06 | 1,774 | 1,864 |
| M2 | 362,90 | 304,61 | 173,92 | 207,20 | 1,596 | 1,902 | |
| M3 | 395,30 | 269,25 | 173,92 | 207,20 | 1,465 | 2,151 | |
| M4 | 388,82 | 261,09 | 173,92 | 207,20 | 1,490 | 2,219 |
Porovnanie experimentálnej odolnosti a odolnosti vypočítanej podľa metód M1 až M4 ukazuje, že skutočná odolnosť prekračuje predpokladanú odolnosť až 1,635násobne v prípade M1 a 1,251násobne pri metóde M2 podľa Tabuľky 4.
| Výpočtový postup | Fmean [kN] | Fmax [kN] |
[–] |
|---|---|---|---|
| M1 | 381,12 | 233,10 | 1,635 |
| M2 | 304,61 | 1,251 | |
| M3 | 269,25 | 1,415 | |
| M4 | 261,09 | 1,460 |
| Súčet reakcií pre smery i | |
|---|---|
| Vx [kN] | Vy [kN] |
| 175,4 | 205,8 |
Tabuľka 5 sumarizuje výsledky maximálnych šmykových napätí (valivý šmyk) od sily 100 kN na účinnej šírke 1 m, podľa výpočtových metód M1 a M3 na 5, 7 a 9vrstvovom CLT panely s pomermi hrúbky lamiel 0,5, 0,75, 1,0, 1,33 a 2,0. Tretí stĺpec skupiny výsledkov je odchýlka výpočtových metód.
Diskusia
Výsledky naznačujú, že k porušeniu dochádza najskôr v smere sekundárneho zaťaženia, čo je v súlade s experimentálnymi pozorovaniami [1].
Je možné pozorovať významný rozdiel v šmykových silách pre rôzne smery i. Tento rozdiel vzniká, pretože metóda M1 sa opiera výlučne o empirické merania z parametrickej štúdie založenej na metóde SAV, uskutočnenej na obmedzenej vzorke s obmedzenými parametrami. Mestekova analýza okamžite predpokladá, že 0,67.n−1 zlomok celkovej sily je rozdelený na hlavnú os CLT, bez ohľadu na pomery rozpätia. To môže viesť k významným nepresnostiam. Na druhej strane metódy M2 až M4 berú do úvahy ohybovú tuhosť a zodpovedajúce rozpätia v rozložení šmykových síl. Presnosť rozloženia síl podľa modelov M2 až M4 bola potvrdená pomocou jednoduchého modelu MKP, ako je znázornené na obrázku 8. Z týchto výsledkov je jasne vidieť, že metódy M2 až M4 vykazujú dobrú zhodu so zjednodušenou analýzou a správne predpovedajú vyššiu šmykovú silu v smer vedľajšej osi CLT dosky a jej hodnoty. Platnosť Musterovej myšlienky rozloženia šmykovej sily bola preukázaná aj v [2] a [10].
| Maximálne napätie vo valivom šmyku | 5vrstvové | 7vrstvové | 9vrstvové | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M1 [MPa] | M3 [MPa] | [%] | M1 [MPa] | M3 [MPa] | [%] | M1 [MPa] | M3 [MPa] | [%] | ||
| dx = 40 mm | dx/dy | 0.833 | 0.822 | 1.389 | 0.667 | 0.662 | 0.741 | 0.501 | 0.498 | 0.564 |
| dy = 20 mm | 0.50 | 1.667 | 1.452 | 14.815 | 0.833 | 0.789 | 5.556 | 0.667 | 0.647 | 2.963 |
| dx = 30 mm | dx/dy | 0.714 | 0.698 | 2.296 | 0.571 | 0.565 | 1.224 | 0.429 | 0.425 | 0.866 |
| dy = 40 mm | 0.75 | 1.429 | 1.288 | 10.884 | 0.714 | 0.686 | 4.082 | 0.571 | 0.559 | 2.177 |
| dx = 40 mm | dx/dy | 0.625 | 0.606 | 3.125 | 0.500 | 0.492 | 1.667 | 0.375 | 0.371 | 1.143 |
| dy = 40 mm | 1.00 | 1.250 | 1.154 | 8.333 | 0.625 | 0.606 | 3.125 | 0.500 | 0.492 | 1.667 |
| dx = 40 mm | dx/dy | 0.714 | 0.686 | 4.082 | 0.571 | 0.559 | 2.177 | 0.429 | 0.423 | 1.462 |
| dy = 30 mm | 1.33 | 1.429 | 1.346 | 6.122 | 0.714 | 0.698 | 2.296 | 0.571 | 0.565 | 1.224 |
| dx = 20 mm | dx/dy | 0.833 | 0.789 | 5.556 | 0.667 | 0.647 | 2.963 | 0.501 | 0.491 | 1.954 |
| dy = 40 mm | 2.00 | 1.667 | 1.607 | 3.704 | 0.833 | 0.822 | 1.389 | 0.667 | 0.662 | 0.741 |
Z výsledkov šmykových napätí vidíme, že Mestekove zjednodušenie konštantného šmykového napätia pozdĺž efektívneho prierezu je veľmi blízke (pozri výsledky M4 a M3. M1 možno zanedbať kvôli nesprávnemu predpokladu šmykovej sily) priamemu výpočtu šmyku. napätie cez Grashofovu rovnicu. Metóda M2 nepopisuje napätia na priereze presne, pri analýze šmykových napätí na CLT nemožno použiť pojem homogénny obdĺžnikový prierez. Tabuľka 5 priamo porovnáva hodnoty šmykových napätí vo valivom šmyku pomocou metód M1 a M2 od jednotkovej sily. V tabuľke je možno pozorovať odchýlky M1 od metódy M3. Rovnaká štúdia bola spracovaná s rôznymi hrúbkami lamiel, s pomer hrúbok lamiel 0,5, 0,75, 1,0, 1,33 a 2,0. Bolo preukázané, že odchýlka pre rovnaký pomer hrúbok lamiel a rovnaký počet vrstiev panela, je vždy rovnaká.
Podhodnotenie kapacity panelu v pretlačení sa pohybuje od 1,25 do 1,64 násobku experimentálnej hodnoty. Najpresnejšia bola metóda M2, napriek nesprávnemu predpokladu šmykových napätí.
Záver
Porovnaním týchto výpočtových metód je preukázané, že žiadna zo súčasne známych metód nedokáže presne opísať poruchu bodovo podoprených CLT panelov pri sústredenom zaťažení. Podhodnotenie kapacity panelu v kompresii sa pohybuje od 1,25 do 1,64násobku experimentálnej hodnoty.
Metódy M1 a M2 majú niekoľko rozdielov. Rozloženie síl podľa Mustera (M2) vykazuje dobrú zhodu s modelom MKP, zatiaľ čo Mestekova metóda je nepresná. Musterovu metódu možno použiť na výpočet šmykovej sily na každej strane podpery, keď sa predpokladá pravidelný stĺpový raster.
Výpočet šmykového napätia v M2 je založený na zjednodušenom Grashofovom vzorci, ktorý predpokladá parabolické rozloženie napätia na homogénnom reze, čo nie je prípad CLT. Navyše výpočet šmykového napätia pre smer x a y používa rovnaké vstupné údaje okrem sily, takže sa neberú do úvahy rôzne prierezové charakteristiky pre každý smer. V Mestekovom prístupe k výpočtu šmykového napätia sa robí aproximácia konštantného šmykového napätia cez efektívnu výšku, po ďalších parametrických štúdiách, ktoré potvrdia malú odchýlku od Grashofovho vzorca, by sa na určenie napätí v šmyku mohla použiť zjednodušená metóda. Na dosiahnutie presných výsledkov by sa však Grashofov vzorec mal používať v jeho nezjednodušenej forme.
Valivá šmyková pevnosť v interakcii s tlakom kolmo na vlákna v blízkosti podpery sa môže podľa Mustera zvýšiť koeficientom 1,6 pre vnútorné stĺpy a 1,3 pre vonkajšie stĺpy, čo experimentálne preukázal vo svojej práci. Napriek tomu však vzorky zlyhávajú pri vyšších hodnotách valivého šmykového napätia. K presvedčivému záveru o zvýšení valivého šmykového odporu pri koncentrovanom zaťažení sa zatiaľ nedospelo.
Je potrebné vykonať ďalšie štúdie, aby sa vyvážila zjednodušená analytická metóda, aby poskytovala presné a ekonomické výsledky.
Literatúra a použité zdroje
- Mestek, Peter 2011. Punktgestützte Flächentragwerke aus Brettsperrholz (BSP) – Schubbemessung unter Berücksichtigung von Schubverstärkungen. [dissertation thesis]. Germany: Technischen Universität München, 2011.
- Muster, M. (2020). Column-Slab Connection In Timber Flat Slabs [dissertation thesis]. Switzerland: ETH ZURICH, 2020.
- Maurer, B., & Maderebner, R. (2021). Cross Laminated Timber under Concentrated Compression Loads - Methods of Reinforcement. Engineering Structures, 245. https://doi.org/10.1016/j.engstruct.2021.112534.
- Mestek, P., & Winter, S. (n.d.). Cross Laminated Timber (CLT)-Reinforcements with Self-Tapping Screws.
- Muster, M., & Frangi, A. (2020). Experimental analysis and structural modelling of the punching behaviour of continuous two-way CLT flat slabs. Engineering Structures, 205. https://doi.org/10.1016/j.engstruct.2019.110046.
- S Zoellig et al. IOP Conf. Ser.: Earth Environ. Sci, 323, 12144. https://doi.org/10.3929/ethz-b-000370480.
- Shahnewaz, Md, et.al. (2023) Experimental research on point-supported CLT panels. Phase 1: rolling shear strength, World conference on Timber Engineering, Oslo 2023. https://doi.org/10.52202/069179-0048.
- A. Hillerborg. Strip Method of Design. 2nd Edition. Cement and Concrete Association, 1975.
https://doi.org/10.1201/9781482271324. - [H. Homberg. Kreuzwerke – Statik der Trägerroste und Platten. Springer-Verlag Berlin Heidelberg, 1951.
https://doi.org/10.1007/978-3-642-52775-3. - Shahnewaz, Md, et.al. (2023) A comparison of punching shear design approaches for point supported CLT panels, World conference on Timber Engineering, Oslo 2023. https://doi.org/10.52202/069179-0349.
Článek se zabývá velmi aktuální a zajímavou problematikou – přehledem stávajících výpočtových metod pro stanovení únosnosti v protlačení desky z křížem vrstveného dřeva, jejich porovnáním a zhodnocením. Požadavky na volnou dispozici uvnitř objektů často vedou k potřebě sloupového nosného systému a souvisejícího lokálního podepření stropních desek. Výzkumu namáhání CLT panelů v nadpodporové oblasti se však dosud věnovala pouze malá pozornost a shrnutí stávajících poznatků v příspěvku je proto užitečné i pro projekční praxi. Vyplývá z něj, že porovnávané výpočtové postupy jsou velmi konzervativní a mohou tak přinášet nehospodárné návrhy, jsou však na straně bezpečnost, a proto použitelné.
Článek je po obsahové i formální stránce zpracován kvalitně. Doporučuji ke zveřejnění.
This publication compares simplified analytical methods for calculating the resistance in compression of a locally supported floor slab made of cross-laminated timber (CLT). The work compares the simplified models according to Mestek and Muster. The reference experiment was taken from Mestek's dissertation. Comparison of these analytical models showed that none of the analytical models could accurately predict the failure of the specimen, leading to uneconomical design.
![Obr. 1 – Na tupo lepený spoj CLT panelov [6]](/docu/clanky/0273/027381o2.png)

![Obr. 3 – Priečny rez porušený panelom z Musterovho experimentu [2]](/docu/clanky/0273/027381o6.png)
![Obr. 4 – Kritický obvod [1]](/docu/clanky/0273/027381o8.png)
![Obr. 5 – Schéma výpočtového modelu [1]](/docu/clanky/0273/027381o10.png)
![Obr. 6 – Referenčný experiment [1]](/docu/clanky/0273/027381o21.png)
![Obr. 7 – Zaťažovací diagram skúšky [1]](/docu/clanky/0273/027381o23.png)