Návrh spriahnutých drevo-betónových konštrukcií v pozemnom a inžinierskom staviteľstve
Spriahnutie drevenej nosnej konštrukcie stropov s tenkou betónovou vrstvou sa objavuje čoraz častejšie u moderných drevostavieb. Takto vytvorená stropná konštrukcia má rad výhodných vlastností oproti bežným dreveným stropom. Spriahnutím sa zvýši predovšetkým statická odolnosť a tuhosť konštrukcie stropu a zlepšia sa jej viaceré stavebnofyzikálne a protipožiarne vlastnosti.
1 Úvod
Spriahnutie drevenej nosnej konštrukcie stropov s tenkou betónovou vrstvou sa objavuje čoraz častejšie u moderných drevostavieb. Takto vytvorená stropná konštrukcia má rad výhodných vlastností oproti bežným dreveným stropom [1]. Spriahnutím sa zvýši predovšetkým statická odolnosť a tuhosť konštrukcie stropu a zlepšia sa jej viaceré stavebno-fyzikálne a protipožiarne vlastnosti.
Spriahnuté drevo-betónové konštrukcie sa môžu úspešne uplatniť aj u drevených mostov a lávok pre peších na zvýšenie statických parametrov mostovky [2]. Súčasne betónová vrstva zabezpečí účinnú konštrukčnú ochranu drevenej časti mostovky od klimatických účinkov.
V príspevku sú uvedené tri príklady použitia spriahnutých drevo-betónových konštrukcií v konkrétnych projektoch vypracovaných v predchádzajúcom období. V dvoch prípadoch sa jedná o konštrukcie stropov a v jednom o mostovku dreveného mosta.
2 Konštrukčné riešenia jednotlivých konštrukcií
2.1 Konštrukcia stropu prístavby Fakulty umení, TU v Košiciach [3]
Obr. 1 Priečny rez prístavbou
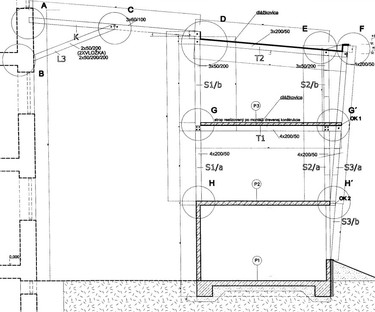
Budova prístavby FU TUKE je navrhnutá s drevenou nosnou konštrukciou od 2.NP. Prízemná časť je z monolitického betónu, na ktorej sú umiestnené jednopoľové dvojpodlažné drevené rámy. Stropná konštrukcia 2.NP je navrhnutá ako betónová doska spriahnutá s drevenými priečľami rámov. V úrovni strešnej konštrukcie sú rámy prepojené s jestvujúcou budovou (obr. 1).
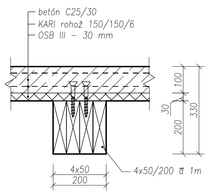
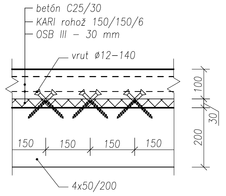
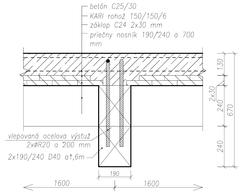
Rámy rozmiestnené vo vzájomnej osovej vzdialenosti 1,0m pozostávajú zo stĺpov a priečlí, ktoré sú zložené z fošní 50/200 použitím klincov. Prierez stĺpov a priečlí na 2.NP je 4×50/200, na 3.NP 3×50/200. Rozpätie rámov je 5500 mm. Na oboch úrovniach je na priečľach upevnený drevený záklop z dosák hrúbky 32 mm. Stropná konštrukcia na 2.NP je spriahnutá drevo-betónová s hrúbkou betónovej dosky 100 mm. Spriahnutie betónovej dosky s drevenými priečlami je zabezpečené pomocou dvojice skrutiek Ø12/140 mm rozmiestnených po dĺžke prievlaku v osovej vzdialenosti 150 mm. Skrutky sú osadené v dreve pod uhlom 45° (obr. 2).
Drevené prvky sú vyrobené zo smrekového dreva pevnostnej triedy SI (C24) s vlhkosťou 18 %. Na betónovú dosku bol použitý betón triedy C25/30.
2.2 Konštrukcia rekonštruovaných stropov na hrade Füzér [4]
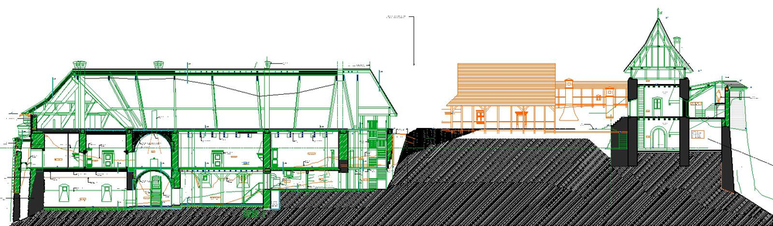
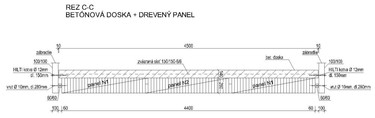
V rámci projektu rekonštrukcie hradu v obci Füzér (Maďarsko) bolo potrebné niektoré stropy navrhnúť v pôvodnom tvare ako trámové s dvojvrstvovým záklopom (obr. 3). Vzhľadom na nové zaťažovacie účinky vyplývajúce z nových funkcií miestností a vzhľadom na súčasné požiadavky spoľahlivosti nosných konštrukcií trámové stropy v pôvodnom konštrukčnom riešení zo statického hľadiska nevyhovovali. Z toho dôvodu sa pristúpilo k spriahnutiu trámového stropu s betónovou doskou, ktorá bola navrhnutá nad dvojitým záklopom. Toto konštrukčné riešenie zabezpečilo výrazné zvýšenie odolnosti a tuhosti konštrukcie stropu a uľahčilo zabezpečiť jej požadovanú požiarnu odolnosť.
Obr. 3 Priečny rez časti hradu
Obr. 4 Konštrukčné riešenie spriahnutého stropu
Rozpätie stropov v jednotlivých miestnostiach je 6,0 resp. 9,0 m. Vzájomná vzdialenosť trámov pri 6,0 m rozpätí je 700 mm a pri 9,0 m je 1600 mm. Hrúbka dosák záklopu je 30 mm, hrúbka betónovej dosky je 130 mm. Nakoľko trámy musia byť z dubového dreva, spriahnutie bolo navrhnuté použitím dvojice vlepovaných tyčí Ø20 mm. Šírka trámov bola určená na 190 mm. Pri rozpätiach 6,0 m vyhoveli trámy 190/240, v prípade stropov s rozpätím na 9,0 m boli navrhnuté spriahnuté drevené trámy 2×190/240. Spriahnutie zabezpečujú tie isté vlepované tyče, ktoré zabezpečujú aj spriahnutie trámu s betónovou doskou (obr. 4).
2.3 Konštrukcia mosta v ZOO v Košiciach [5]
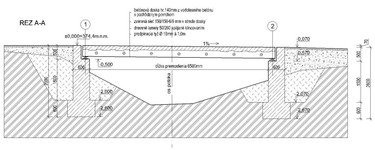
Objekt mosta sa nachádza v rámci areálovej komunikácie ZOO KE. Je navrhnutý cez tok potoka s dĺžkou premostenia 6,5 m. Šírkové usporiadanie mosta je 4,5 m, je prispôsobené možnosti prípadnému prechodu obslužným vozidlám s max. hmotnosťou 12 t, ale predovšetkým slúži pre pešiu komunikáciu. Most je navrhnutý so spriahnutou drevo-betónovou doskovou mostovkou. Mostovka je uložená na železobetónových pilieroch na oboch brehoch potoka. Na mostovke nie je uložený žiadny mostný zvršok, povrch betónovej vrstvy mostovky je vyhladený aby bol pochôdzny. Zábradlie je drevené.
Obr. 5 Pozdĺžny rez mostom
Obr. 6 Priečny rez mostovkou
Samotná mostovka s rozmermi 4,5×7,0 m je vytvorená z 260 mm hrubej masívnej drevenej dosky, zloženej z vertikálne ukladaných, vzájomne sklincovaných lamiel 50/260 mm a z betónovej dosky hrúbky 140 mm. Ich vzájomné statické spolupôsobenie je zabezpečené prostredníctvom 2× 4 drážok hĺbky 30 mm vyrezaných naprieč celej šírky v drevenej časti mostovky. Drevená časť mostovky z montážnych dôvodov pozostáva z troch častí – dielcov 2× N1 a N2. Tie po uložení na pilier budú navzájom spojené pomocou predpínacích tyčí – závitové tyče Ø16, ktoré sa prevlečú cez vopred vyvŕtané otvory naprieč mostovky (obr. 5). Drevené nosné prvky sú navrhnuté zo smrekového dreva pevnostnej triedy SI (C24). Vlhkosť dreva je 18 %. Fošne lamelovanej dosky musia byť z jedného kusu po celej dĺžke mostovky a musia byť hobľované. Betónová doska mostovky je z vodotesného betónu triedy C 25/30.
3 Použitý výpočtový model
Na dimenzovanie a posúdenie vyššie uvedených spriahnutých drevo-betónových sústav bol použitý analytický výpočtový model v súlade s STN EN 1995-1-1 [7] nazývaný aj ako „γ-metóda“, ktorý zohľadňuje poddajnosť spriahovacích prostriedkov zavedením tzv. efektívnej tuhosti prierezu:
,
(1)
kde je
- γ
- – súčiniteľ poddajnosti spriahnutia.
Do výpočtu účinnej ohybovej tuhosti prierezu bolo zavedené viskózno-pružné dotvarovanie betónu podľa smernice CEB-FIB 1990 uvedené v európskej norme pre navrhovanie betónových konštrukcií [6]. Viskózno-pružné a mechanicko-sorpčné dotvarovanie dreva bolo zohľadnené reologickým modelom podľa Torattiho [8]. Pre dotvarovanie spriahovacích prostriedkov bol navrhnutý všeobecný vzťah použiteľný pre rôzne druhy spriahovacích prostriedkov φs
,
(2)
kde je
- φc
- – súčiniteľ dotvarovania betónu,
- φt
- – súčiniteľ dotvarovania dreva.
Tento vzťah môže byť použitý pre výpočet súčiniteľa dotvarovania rôznych druhov spriahnutia a zohľadňuje dotvarovanie oboch spájaných materiálov, dreva a betónu.
Obr. 7 Silové pôsobenie a priebeh napätí v spriahnutom priereze od zmrašťovania betónu
Pre stanovenie účinkov zmrašťovania betónu a pretvorení v dôsledku teplotných a vlhkostných zmien prostredia boli odvodené vzťahy pre výpočet priehybu nosníka v strede rozpätia a priebehu napätí v najviac namáhanom priereze.
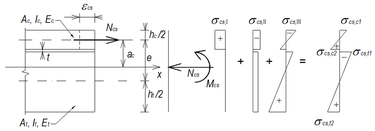
Priebeh napätí v spriahnutom drevo-betónovom priereze vplyvom zmrašťovania σcs, sa určí sčítaním príslušných napätí σcsI, σcsII, a σcsIII (obr. 7) pomocou nasledujúcich vzťahov:
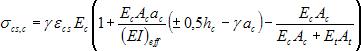(3)
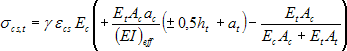(4)
kde je
- εcs
- – pomerné pretvorenie betónu v dôsledku zmrašťovania,
- γ
- – súčiniteľ poddajnosti spriahnutia.
Priehyb v strede rozpätia spriahnutého prostého nosníka sa vplyvom zmrašťovania betónu zvýši o hodnotu
.
(5)
Podobne boli odvodené vzťahy pre výpočet účinkov vplyvu zmien teploty a relatívnej vlhkosti prostredia na priebeh napätí a priehybu spriahnutých drevo-betónových nosníkoch s poddajným spriahnutím.
Pomocou vypracovaného modelu [9] je možné stanoviť časový priebeh napätí v spriahnutom drevo-betónovom priereze a priehyb v strede rozpätia nosníka so zohľadnením jednotlivých reologických javov.
4 Analýza priehybov prezentovaných spriahnutých sústav
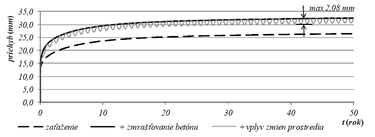
Pri posudzovaní spoľahlivosti spriahnutých drevo betónových sústav nad určité rozpätie (cca 6,0 m) je rozhodujúcim kritériom II. medzný stav, tj. priehyb konštrukcie. Keďže časovo závislé reologické vlastnosti dreva a aj betónu pri dlhodobom pôsobení ovplyvnia predovšetkým priehyb, bola uskutočnená analýza prezentovaných spriahnutých sústav pri ich dlhodobom pôsobení. Predmetom analýzy bolo zistiť ako vyšetrované konštrukcie postupne zväčšujú svoj priehyb v čase, resp. aké sú ich priehyby od rôznych druhov zaťažení. Konečný priehyb bol určený v časovom intervale 50 rokov. Keďže betón a drevo sú materiály s odlišnými teplotnými a vlhkostnými vlastnosťami, pravidelné zmeny teploty a vlhkosti prostredia spôsobujú pravidelné výchylky priehybu v priebehu roka.
4.1 Konštrukcia stropu prístavby Fakulty umení, TU v Košiciach
Obr. 8 Priebeh priehybu stropu v čase
| počiatočný priehyb od kvázi stáleho zaťaženia | 5,42 mm |
| konečný priehyb od kvázi stáleho zaťaženia | 22,00 mm |
| konečný priehyb od zmrašťovania | 6,02 mm |
| konečný priehyb od stáleho zaťaženia | 28,03 mm |
| globálny súčiniteľ dotvarovania | 4,2 |
| celkový počiatočný priehyb (aj s prevádzk. zaťaž.) | 9,94 mm |
| podiel z rozpätia L = 5500 mm | 1/553 |
| celkový konečný priehyb (aj s prevádzk. zaťaž.) | 32,50 mm |
| podiel z rozpätia L = 5500 mm | 1/169 |
| odchýlky priehybu vplyvom zmien vlhkosti a teploty | 2,08 mm |
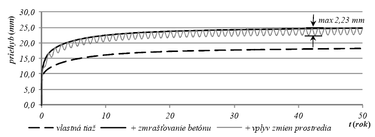
4.2 Konštrukcia rekonštruovaných stropov na hrade Füzér
Strop s rozpätím L = 6,3 m
Obr. 9 Priebeh priehybu stropu v čase
| počiatočný priehyb od kvázi stáleho zaťaženia | 4,52 mm |
| konečný priehyb od kvázi stáleho zaťaženia | 16,36 mm |
| konečný priehyb od zmrašťovania | 6,49 mm |
| konečný priehyb od stáleho zaťaženia | 22,85 mm |
| globálny súčiniteľ dotvarovania | 4,1 |
| celkový počiatočný priehyb (aj s prevádzk. zaťaž.) | 6,49 mm |
| podiel z rozpätia L = 6300 mm | 1/970 |
| celkový konečný priehyb (aj s prevádzk. zaťaž.) | 24,80 mm |
| podiel z rozpätia L = 6300 mm | 1/254 |
| odchýlky priehybu vplyvom zmien vlhkosti a teploty | 2,23 mm |
| počiatočný priehyb od kvázi stáleho zaťaženia | 10,77 mm |
| konečný priehyb od kvázi stáleho zaťaženia | 25,1 mm |
| konečný priehyb od zmrašťovania | 14,2 mm |
| konečný priehyb od stáleho zaťaženia | 39,3 mm |
| súčiniteľ dotvarovania | 2,6 |
| celkový počiatočný priehyb (aj s prevádzk. zaťaž.) | 15,46 mm |
| podiel z rozpätia L = 9000 mm | 1/582 |
| celkový konečný priehyb (aj s prevádzk. zaťaž.) | 44,0 mm |
| podiel z rozpätia L =9 000 mm | 1/205 |
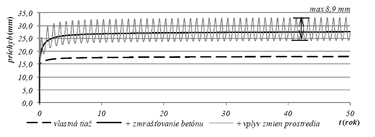
4.3 Konštrukcia mosta v ZOO v Košiciach
Obr. 10 Priebeh priehybu mostovky v čase
| počiatočný priehyb od vlastnej tiaže | 1,5 mm |
| konečný priehyb od vlastnej tiaže | 5,5 mm |
| konečný priehyb od zmrašťovania | 9,6 mm |
| konečný priehyb od stáleho zaťaženia | 15,1 mm |
| súčiniteľ dotvarovania | 9,0 |
| celkový počiatočný priehyb (aj s prevádzk. zaťaž.) | 14,13 mm |
| podiel z rozpätia L = 6800 mm | 1/481 |
| celkový konečný priehyb (aj s prevádzk. zaťaž.) | 27,49 mm |
| podiel z rozpätia L = 6800 mm | 1/247 |
| odchýlky priehybu vplyvom zmien vlhkosti a teploty | 8,9 mm |
5 Záver
Výsledky analýzy pri dlhodobom pôsobení spriahnutých drevo-betónových nosníkov ukázali výrazný nárast priehybu v čase. Nezanedbateľný vplyv na ich priehyb má zmrašťovanie betónu. V prípade analyzovaných stropných konštrukcií je odhadované zvýšenie priehybu vplyvom zmrašťovania betónu o hodnotu 6,0 až 6,5 mm, pri mostovke je to 9,6 mm, čo je v porovnaní s počiatočným priehybom významná hodnota. Nárast priehybu vyšetrovaných konštrukcií od dlhodobého zaťaženia v čase 50 rokov sa predpokladá 1,9 až 3,8násobný. Časový priebeh nárastu priehybov uvedených konštrukcií je uvedený na obr. 7 až obr. 9. Z týchto grafov vyplýva, že cca 95 % z celkového nárastu priehybu konštrukcií sa dosiahne už za prvých 7 až 10 rokov.
Z uvedených výsledkov vyplýva, že u drevo-betónových sústavách vplyv dlhodobého účinku zaťaženia je nezanedbateľný a je s ním potrebné uvažovať návrhu konštrukcií.
Tento článok vznikol v rámci riešenia grantového projektu č. 1/0865/11 podporovaného VEGA MŠ.
6 Literatúra
- [1] Kanócz, J.: Spriahnuté drevo-betónové sústavy a ich použitie v praxi, Stavebné materiály, ročník III, 06/2007, ISSN 1336-7616, pp. 42-43.
- [2] Kanócz, J.: Progresívne statické a konštrukčné riešenia drevených mostov a lávok, Zborník z odborného seminára so zahraničnou účasťou, Dřevostavby – stavební systém budoucnosti, Volyně, ČR, 12-13.04.2006, ISBN 80-86837-03-3.
- [3] Prístavba Fakulty umení Technickej univerzity v Košiciach, Projekt stavby, Košice 2012. Autor: doc. Ing. arch. Juraj Koban, Statika: doc. Ing. Marián Rovňák, PhD., doc. Ing. Ján Kanócz, CSc.
- [4] Rekonštrukcia hradu v obci Füzér, Projekt stavby, Miskolc, 2013. Autor: Ing. arch. Rudolf Mihaly, DLA , Statika: Ing. Kálydy Zoltán, doc. Ing. Ján Kanócz, CSc., Ing. Viktória Bajzecerova, PhD.
- [5] Most v ZOO Košice, Projekt stavby, Košice 2012. Autor: doc. Ján Kanócz, CSc., Statika: doc. Ing. Ján Kanócz, CSc., Ing. Viktor Bauer.
- [6] STN EN 1992-1-1: Navrhovanie betónových konštrukcií. Všeobecné pravidlá a pravidlá pre budovy
- [7] STN EN 1995-1-1: Navrhovanie drevených konštrukcií. Všeobecné pravidlá a pravidlá pre budovy
- [8] Toratti, T.: Creep of timber beams in variable environment. PhD thesis, Helsinki University of Technology, Laboratory of Structural Enginieering and Building Physics, 1992.
- [9] Kanócz J., Bajzecerová V.: Influence of rheological behaviors to load-carrying capacity of timber-concrete composite beams under long term loading. In: Procedia Engineering. Vol. 40 (2012), p. 20-25. ISSN 1877-7058 Spôsob prístupu: http://www.sciencedirect.com/science/article/pii/S1877705812024356
In this paper, three different projects of timber-concrete composite structures are presented – floor structure of new building, floor slab of rebuilt castle and deck plate of the short span bridge. Load carrying capacity of the timber-concrete composite structural elements is influenced with various rheological factors. For their optimal design number of these factors has to be taken in to account. In the case of presented project analytical model for long term loading developed by authors was applied. The time depending analysis shows a significant influence of creep of materials, mechano-sorptive creep of timber, but mostly concrete shrinkage on the final mid span deflection.