Měření základních fyzikálních veličin potřebných při měření emisí znečišťujících látek – 1. část
Příspěvek se věnuje problematice měření průtoku plynu v uzavřeném profilu. Zabývá se fyzikálním principem měření a také odkazuje na normované postupy zabývající se touto problematikou. Dále je v krátkosti pojednáváno o principech měření teplot a tlaků, které jsou pro měření průtoku nezbytnými stavovými veličinami.
1. Úvod
V rámci činností a úkonů prováděných při měření emisí je potřeba často měřit nejrůznější fyzikální veličiny. Výčet všech fyzikálních veličin je značně rozsáhlý (je možno jej nalézt např. v každé učebnici fyziky). Cílem tohoto příspěvku je zaměřit se pouze na ty veličiny, jež jsou nejčastěji měřeny při emisních měřeních. Proto se v následujícím příspěvku budeme podrobně věnovat pouze měření průtoků se zaměřením na měření průtoku spalin a vzdušin pomocí rychlostních sond a stručně principům měření tlaků a teplot (stavové veličiny).
2. Podmínky a způsob měření průtoků spalin a vzdušin
2.1. Pojmy, jednotky a principy měření průtoku tekutin
Tekutinami nazýváme látky, jejichž nejmenší částice se navzájem snadno přemisťují. Přitom rozlišujeme kapaliny, jejichž objem jen velmi málo podléhá vlivu změny tlaku a teploty, od vzdušin neboli plynů a par, které se naopak vyznačují značnou stlačitelností i tepelnou roztažností. Kapaliny, jejichž hlavním představitelem je voda, jsou předmětem studie hydromechaniky. Chování stlačitelných tekutin, zvláště vzduchu, sleduje aeromechanika. Pokud se přitom uplatňuje vliv tepla nebo teploty, stává se mechanika plynů a par součástí termomechaniky [5].
Pod pojmem měření průtoku tekutin rozumíme stanovení proteklého objemu ![]() (objemový průtok) nebo hmoty Δm (hmotnostní průtok) v určitém průřezu A za časovou jednotku τ [2].
(objemový průtok) nebo hmoty Δm (hmotnostní průtok) v určitém průřezu A za časovou jednotku τ [2].
Objemový průtok:
Hmotnostní průtok:
kde je

- – průměrná rychlost v průřezu v m/s,
- A
- – plocha průřezu potrubí (výduchu) v místě měření v m2,
- ρ
- – hustota proudící tekutiny v kg/m3.
Při přepočtu průtoku na časovou jednotku lišící se od jednotky, během které se průtok stanovoval, musíme ovšem předpokládat, že okamžitý průtok (jako limitní případ: Δτ → 0) zůstává po celou dobu nezměněn. Ze vztahů (1) a (2) je zřejmé, že objemový a hmotnostní průtok (při známé hustotě ρ tekutiny a ploše průřezu A) můžeme určit buď na základě měření objemu nebo rychlosti (nepřímé měření průtoků).
K měření průtočného množství se používá měřidel založených na nejrůznějších fyzikálních principech [2], [4]:
- průběžně nebo přetržitě pracující objemové průtokoměry (měří objem tekutiny, který proteče za určitý čas),
- rychlostní průtokoměry (užití v uzavřených kruhových kanálech; oběžné kolo průtokoměru je poháněno proudem měřené tekutiny a počet otáček je úměrný rychlosti proudění a tedy i průtoku; Woltmanův průtokoměr; Ottovo hydrometrické křídlo),
- mechanické nebo žhavené anemometry,
- rychlostní sondy, měření rychlosti a vektoru rychlosti proudící tekutiny (měření dynamického tlaku v proudící tekutině, ČSN ISO 10780),
- průřezová měřidla (při zmenšení průtokového průřezu nastane lokální zvětšení kinetické energie na úkor tlakové energie, změna tlakové diference statických tlaků před a za škrtícím orgánem je funkcí průtoku; ČSN ISO 5167-1),
- plováčkové průtokoměry, rotametry (patří mezi škrtící prvky, ale na rozdíl od clon, dýz a Venturiho trubice to je měřidlo s konstantním průtokovým průřezem, kde změna průtoku způsobí změnu tlakové diference, u rotametrů průtoková změna způsobí změnu průtokového průřezu a tlaková diference v místě měření zůstává konstantní),
- kolenový průtokoměr (působením odstředivé síly vzniká při průtoku tekutiny kolenem tlaková diference, měřená v ose souměrnosti kolena, která je funkcí průtoku),
- indukční průtokoměry (při pohybu elektrického vodiče, proud elektricky vodivé tekutiny, v magnetickém poli se ve vodiči indukuje napětí, které je funkcí rychlosti proudící tekutiny),
- ultrazvukové průtokoměry (využívají závislosti rychlosti šíření ultrazvuku v tekutinách na směru a rychlosti proudící tekutiny),
- hmotnostní průtokoměry (na rozdíl od výše uvedených principů měřidel, pomocí kterých stanovujeme hmotnostní průtok nepřímo, je hmotnostní průtokoměr měřidlo přímé tzn. hmotnostní průtok je přímo měřenou veličinou).
Volbu nejvhodnější metody měření průtoku v konkrétním případě ovlivňují níže popsané okolnosti:
- podmínky měření (tvar, velikost, dostupnost měřícího místa, možnost manipulace),
- fyzikální a chemické vlastnosti protékajících tekutin,
- tlak a teplota protékajících tekutin,
- kvantitativní parametry protékajících tekutin (maximální a minimální hodnota průtoku a jeho časové změny),
- požadovaná přesnost měření,
- účel měření (jednorázové, kontinuální, provozní, informativní),
- požadavky na záznam či využití signálu pro regulaci.
2.2. Měření průtoků spalin a vzdušin pomocí rychlostních sond
Protože se v praxi pro stanovení průtoku spalin a vzdušin při jednorázových měřeních nejčastěji používají rychlostní sondy [8], bude se další část zabývat podrobněji touto oblastí.
2.2.1. Teoretický rozbor principu
Pro proudění ve vodorovné trubici platí pro dokonalou tekutinu Bernoulliho rovnice:
kde je
- ps
- – statický tlak tekutiny v Pa,
- pc
- – celkový tlak tekutiny v Pa,
- ρ
- – hustota tekutiny při aktuálním tlaku a teplotě v kg/m3,
- v
- – rychlost proudění tekutiny v m/s.
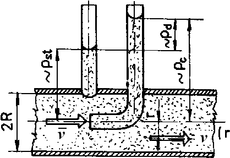
Trubka, která je vložena do proudící tekutiny tak, aby její ústí stálo kolmo na směr proudu, bude udávat celkový tlak pc, protože v otvoru trubky se změní kinetická energie proudu na dynamický tlak pd. V proudící tekutině (kapalina, plyn nebo pára) vedle statického tlaku pst působí ještě i tlak dynamický pd. Zatímco pst je veličinou skalární (působí stejně všemi směry), pd je vektorem, který v daném bodě má totožný směr jako vektor rychlosti proudu. Součet (vektorový) obou tlaků se nazývá celkovým tlakem pc a jeho (skalární) velikost v případě podle obr. č. 1 je [1]:
Za předpokladu, že v celém průřezu A je stejná střední rychlost, pak můžeme dynamický tlak pd (v souladu s Bernoulliho rovnicí) vyjádřit vztahem:
Rychlost pohybující se částice tekutiny je v případě prostorového proudění vektor ![]() určený třemi složkami vx,y.z ve zvoleném souřadnicovém systému. Uvažujeme-li, že je v průřezu jednorozměrné proudění v = vx, pak ze vztahu (6) vyplývá, že tato rychlost proudění je:
určený třemi složkami vx,y.z ve zvoleném souřadnicovém systému. Uvažujeme-li, že je v průřezu jednorozměrné proudění v = vx, pak ze vztahu (6) vyplývá, že tato rychlost proudění je:
Vztah (7) pro rychlost platí přesně pouze pro proudění nestlačitelných tekutin nebo plynů s malou rychlostí. Při průtoku s větší rychlostí platí:
kde je
- ε
- – kompresní faktor, který lze přibližně vypočítat ze vztahu:
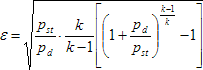 (9)
[–]
(9)
[–]
kde je
- k
- – izoentropický exponent (pro vzduch má hodnotu 1,4).
V obou případech lze tedy měření rychlosti převést na měření tlaku (pd, pst), známe-li určité fyzikální vlastnosti tekutiny. Nejjednodušší a nejstarší zařízení pracující na tomto principu byla Pitotova trubice. Šlo v podstatě o již naznačený způsob snímání celkového a statického tlaku. Stejně jako na obr. č. 1 byly tyto údaje získávány z různých míst [1].
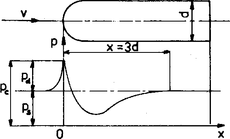
Rychlostní sondu pro měření tlaků pst a pc prakticky v jediném místě navrhl Prandtl. Tato sonda byla navržena se zřetelem na rozdělení tlaku na povrchu obtékaného rotačního tělesa, které by vzniklo složením rovnoběžného proudu a bodového zdroje. Na čele rotačního tělesa se celá rychlost nerušeného proudu mění v dynamický tlak, takže celkový tlak je tam největší. Dále na křivém povrchu tělesa tlak značně klesá, protože zhuštěním proudnic se tu zvyšuje rychlost. Potom v dostatečné vzdálenosti od čela se opět zvýší na hodnotu přibližně rovnou statickému tlaku v nerušeném proudu (viz obr. č. 2). Pro usnadnění výroby a vzhledem k tomu, že se proudění skutečných tekutin poněkud liší od předpokládaného potenciálního obtékání, nahrazuje se teoretický tvar válcem průměru d s půlkulovým zakončením [1].
Tlakový rozdíl vznikající mezi otvorem na čele a štěrbinami na obvodu je relativně malý, čímž je limitováno i její použití při malých rychlostech (tlacích) tekutiny. Prandtlova trubice není vhodná pro samotné určení směru rychlosti proudění. K tomuto účelu lze použít buď válcové nebo kulové sondy [1].
2.2.2. Rozložení rychlostního pole
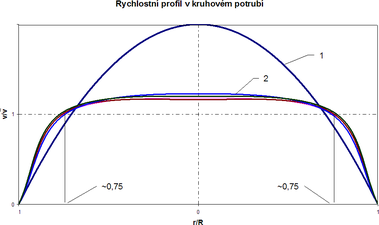
Obr.č. 3 Rychlostní profil v kruhovém potrubí
1 – laminární (parabola), 2 – Turbulentní proudění (Re od 4 000 do 108)
U ideálně vyvinutého rychlostního profilu (při laminárním i turbulentním proudění) možno přibližně určit měřením v místě vzdáleném o ¼ R od vnitřní stěny potrubí (viz obr. č. 3) [5].
2.2.3. Normativní předpisy pro měření rychlosti a průtoku tekutin v potrubí
V současné době existuje více platných standardních předpisů, jejichž součástí je stanovení rychlosti a průtoku tekutin pomocí rychlostních sond, např.:
- ČSN 12 3061, Vzduchotechnika, Ventilátory – Předpisy pro měření (účinnost od 11/1987),
- ČSN 12 4070, Zařízení Odlučovací – Metody měření veličin (účinnost od 01/1990),
- ČSN ISO 10780, Stacionární zdroje emisí – Měření rychlosti a průtoku plynů v potrubí (účinnost od 07/1998),
- ČSN ISO 16911-1, Stacionární zdroje emisí – Manuální a automatické stanovení rychlosti proudění a průtoku plynů v potrubí – Část 1: Manuální referenční metoda (účinnost od 09/2013).
V další části příspěvku bude (z pohledu praktického využití) podrobněji popsán a rozebrán postup a podmínky měření rychlosti a průtoku uvedený v ČSN ISO 10780.
2.2.4. Měření rychlosti a průtoku plynů v potrubí dle principů uvedených v ČSN ISO 10780 [6]
Tato mezinárodní norma specifikuje manuální metody pro stanovení rychlosti a průtoku plynů v potrubí, výduších a komínech, které ústí do atmosféry. Pozn.: dále uvedené značky veličin vycházejí z normy.
Podstata měření
Průměrná rychlost proudu se zjišťuje pomocí Prandtlovy trubice změřením hodnoty rychlosti v ve zvolených bodech průřezu potrubí. Průtok qv se vypočítá vynásobením plochy průřezu průměrnou rychlostí proudu plynu v tomto průřezu. Tato metoda sestává z:
- určení rozměrů potrubí v místě měření,
- určení počtu n a umístění x měřicích bodů potřebných k odpovídajícímu zjištění rychlostního profilu v celém průřezu potrubí,
- změření diferenčního tlaku Δp v otvorech Prandtlovy trubice umístěné v těchto měřicích bodech,
- stanovení průměrných hodnot hustoty (nebo molární hmotnosti), teploty, statického a diferenčního tlaku pro výpočet průměrné rychlosti plynu,
- výpočtu průtoku, který vychází ze zjištěné průměrné rychlosti a plochy průřezu.
Doporučené typy rychlostních sond
Norma doporučuje dva typy Prandtlovy trubice.
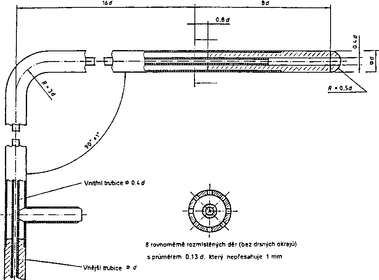
Typ „L“ (viz obr. č. 4) detailněji popsaný v ČSN ISO 10780 je považovaný za standardní rychlostní sondu. Tento typ je také známý jako Prandtlova-Pitotova sonda. Základním požadavkem při měření je rovnoběžnost osy vstupního otvoru (hlavy sondy) s osou kanálu (proudu) v místě měření. Při měření celkového a statického tlaku se při odklonu sondy od směru proudu do ±5° velikost naměřených hodnot prakticky nemění. Při měření dynamického tlaku je jeho hodnota prakticky stálá do odklonu ±15°. Pokud je sonda vyrobena dle nákresu, je její konstanta K = 0,99±0,01, což v podmínkách provozních měření představuje K = 1. Její nevýhodou je dlouhá hlava (24d), a to si vyžaduje ve stěně potrubí poměrně velký otvor (čím je stěna širší, tím větší musí být otvor).
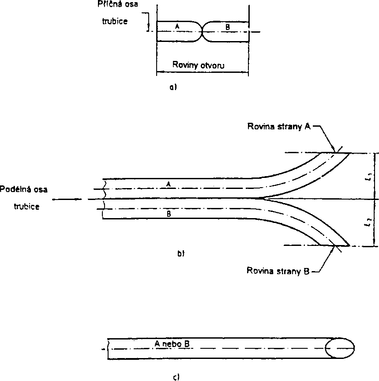
Prandtlova trubice typu „S“ (obr. č. 5) se velmi často používá při proměřování komínů, protože je vhodná k měření spojenému s odběrem vzorku a také proto, že je robustní, malá a snadno zhotovitelná (výhoda potřeby menšího otvoru pro zasunutí do potrubí roste se zvětšující se šířkou stěny potrubí). Pokud je sonda vyrobena dle nákresu, je její konstanta K = 0,84±0,01. Někdy se sonda typu „S“ kombinuje se sondou na odběr vzorku (izokinetický odběr vzorku tuhých látek) a teplotním čidlem. Pro takovéto užití jsou v normě uvedeny minimální rozteče mezi jednotlivými měřícími prvky z ohledem na minimalizaci chyb měření průtoku.
Pokud nejsou dodrženy konstrukční požadavky pro jednotlivé typy Prandtlovy trubice, musí být kalibrační faktor K stanoven kalibrací pomocí standardní Prandtlovy trubice, která odpovídá ČSN ISO 10780.
Požadavky na prostředí
Celková chyba spojená s měřením rychlosti v potrubí při použití výše uvedených sond bude menší než 3 % při dodržení následujících podmínek:
- Reynoldsovo číslo proudu plynu na povrchu Prandtlovy trubice musí být větší než 1200 a rychlost proudu plynu se musí pohybovat v rozmezí 5 až 50 m/s. Při hodnotách Reynoldsova čísla menších než 1200 jsou Prandtlovy trubice náchylné ke značným chybám. Při rychlostech vyšších než 50 m/s má Prandtlova trubice sklon k vibracím nebo dochází k jejímu vyosení, což také může způsobit značné chyby při měření tlaku.
- Úhel víření proudu plynu nesmí být v žádném bodě měřené plochy průřezu potrubí odkloněn o více než ±15° od osy proudění rovnoběžné s osou proudění (metoda zjišťování výskytu víření a metoda pro vyrovnání proudu plynu je popsána v příloze normy).
- Proud plynu nesmí vykazovat žádné pravidelné ani cyklické kolísání tlaku. Zjištěné odchylky od střední hodnoty nesmí v daném bodě přesáhnout ±24 Pa. Malé kolísání tlaku je přirozené a je zahrnuto v tlaku odečteném na manometru.
- V případě kruhového průřezu potrubí se měření musí provést nejméně ve dvou měřicích přímkách, které svírají pravý úhel. Rozdíl mezi průměrnými rychlostmi v obou měřených bodech nesmí překročit 5 %. V případě překročení pětiprocentní hranice musí být provedeno nové měření v jiném profilu nebo vybráno jiné místo potrubí (v praxi velice problematická realizace).
- Vnitřní průměr potrubí musí být znám s přesností do 1 % délky přímého úseku potrubí.
- Ve vzdálenosti nejméně pěti hydraulických průměrů proti proudu a pěti hydraulických průměrů po proudu od roviny měření rychlosti (měřicího profilu) nesmí potrubí vykazovat žádné změny vnitřního průměru (v praxi nemožnost ověření).
- V žádném bodě měřicího profilu se během měření Prandtlovou trubicí nesmí vyskytnout zpětný tok.
- Rozdíly teploty měřeného plynu při měření rychlosti nesmí přesáhnout 5 % průměrné absolutní teploty v měřicím profilu (větší odchylky ukazují na výskyt zvrstvení toku v místě měření).
Postup měření
Rekognoskace
Před provedením měření se ujasní účel měření s objednavatelem včetně seznámení se s technologií. Jestliže výrobní proces může probíhat ustáleně, musí být v tomto stavu udržován tak, aby bylo dosaženo optimálních podmínek měření. Rekognoskace zadaného zařízení usnadní výběr nejvhodnějšího měřicího profilu a určení požadovaného počtu a rozmístění vzorkovacích bodů.
Volba měřicího profilu
Měření musí probíhat v přímém úseku potrubí s konstantním tvarem a plochou průřezu, co nejdále po směru toku od jakýchkoli překážek, které by mohly způsobit poruchy nebo změny směru toku. Pro zajištění rovnoměrného rozdělení rychlosti plynu v rovině měření musí mít přímý úsek potrubí délku rovnou přinejmenším sedminásobku hydraulického průměru potrubí (v praxi někdy nesplnitelné). Na tomto přímém úseku potrubí se umístí měřicí profil ve vzdálenosti pěti hydraulických průměrů od počátku tohoto úseku. Pokud je měřicí profil umístěn v blízkosti výstupu proudu plynu do atmosféry, má být jeho vzdálenost od konce přímého úseku potrubí také pět hydraulických průměrů (pro nekruhová potrubí je hydraulický průměr vypočítán vynásobením plochy průřezu potrubí čtyřmi a dělením výsledné hodnoty velikostí jeho obvodu).
Počet měřicích bodů
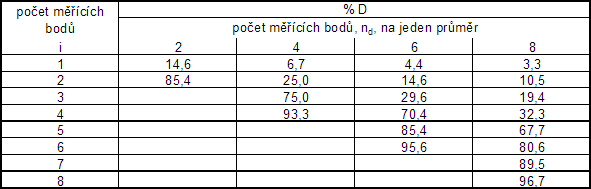
Minimální počet měřicích bodů je určen rozměry měřicího profilu. Obecně tento počet stoupá s rostoucí plochou průřezu potrubí. Nejmenší počet potřebných vzorkovacích bodů je uveden v tab. č. 1 a 2 pro potrubí kruhového a čtyřhranného průřezu.
Tab. č. 1 Nejmenší počet měřicích bodů pro potrubí kruhového průřezu

Tab. č. 2 Nejmenší počet měřicích bodů pro potrubí čtyřhranného průřezu

Umístění měřicích bodů
Plocha měřicího profilu musí být rozdělena na rovnoploché části a měření rychlosti musí být provedeno ve středu každé části. Žádný z měřicích bodů nesmí ležet ve vzdálenosti menší než 20 mm od stěny potrubí. Pokud se tento případ vyskytne, musí být Prandtlova trubice umístěna 20 mm od stěny potrubí.
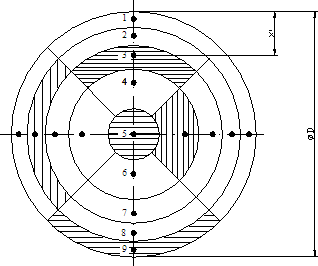
Obr. č. 6 Rozmístění měřicích bodů v potrubí kruhového průřezu – Základní rozdělení
Poznámka – Šrafované části mají stejnou plochu (rozmístění pro D > 2 m)
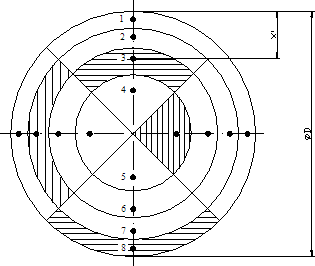
Obr. č. 7 Rozmístění měřicích bodů v potrubí kruhového průřezu – Tangenciální rozdělení
Poznámka – Šrafované části mají stejnou plochu (rozmístění pro D >2 m)
Pro rozdělení potrubí kruhových průřezů norma uvádí dvě možnosti. Obě rozdělují průřez potrubí na rovnoploché části. Při základním rozdělení je na rozdíl od tangenciálního rozdělení měřicí bod umístěn ve středu průřezu. Základní a tangenciální rozmístění v potrubí kruhového průřezu je uvedeno na obr. č. 6 a 7. Rozmístění měřicích bodů v potrubí čtyřhranného průřezu je uvedeno na obr. č. 8. Vzdálenosti měřicích bodů v procentech průměru D od stěny potrubí jsou uvedeny v tab. č. 3 a 4.
Tab. č. 3 Vzdálenost měřicích bodů od stěny potrubí – Základní rozdělení
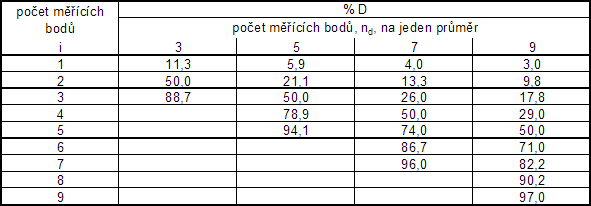
Tab. č. 4 Vzdálenost měřicích bodů od stěny potrubí – Tangenciální rozdělení
Měření
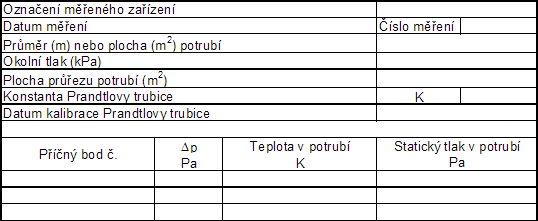
Po příslušných přípravách (plošina, měřící otvory, označení měřicích bodů na sondě, připojení tlakoměru) se při vlastním měření změří a zapisuje v každém měřicím bodě:
- statický tlak,
- dynamický tlak (dle normy označen jako diferenční tlak Δp),
- teplota T.
Dále se změří a zapíše atmosférický tlak pamb. Možný vzor formuláře pro zápis výše uvedených údajů je označen jako tab. č. 5.
Tab. č. 5 Příklad formuláře pro zápis měřených hodnot
Výpočet rychlosti a průtoku
Průměrná teplota tekutiny v měřeném průřezu se vypočte jako aritmetický průměr dle vztahu:
kde je
- Ti
- – absolutní teplota v bodě i v K.
Průměrná hodnota statického tlaku ze všech měřicích bodů se vypočte jako aritmetický průměr dle vztahu:
kde je
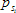
- – statický tlak v bodě i v kPa,
- n
- – počet měřicích bodů.
Absolutní statický tlak tekutiny v potrubí se stanoví dle vztahu:
kde je
- pamb
- – atmosférický tlak v místě a čase měření v kPa.
Průměrná hodnota diferenčního tlaku Δp naměřeného Prandtlovou trubicí se stanoví dle vztahu (upravený vztah pro výpočet kvadratického průměru):
kde je
- Δpi
- – diferenční tlak v bodě i v kPa.
Průměrná rychlost tekutiny v měřeném průřezu se vypočítá dle vztahu:
kde je
- K
- – konstanta Prandtlovy trubice (kalibrační faktor),
- C
- – konstanta, C = 129 m‧kg½‧kmol−(½)‧K−(½)‧s−1,
- M
- – molární hmotnost plynu, pokud M leží v rozmezí od 27 do 31 kg/kmol, lze počítat s hodnotou 29 kg/kmol.
Vztah pro výpočet konstanty C odvodíme dosazením vztahu pro výpočet hustoty ρ tekutiny z molární hmotnosti (při efektivních podmínkách) do vztahu (7), který násobíme konstantou Prandtlovy trubice. Výsledný vztah pak je:
kde je
- VN
- – objem kilomolu plynu při norm. podmínkách VN = 22,4 v m3/kmol,
- TN
- – teplota plynu při norm. podmínkách TN = 273 v K,
- pN
- – tlak plynu při norm. podmínkách pN = 101 325 v Pa.
S ohledem na odvození vztahu (14) je možno říci, že pokud do tohoto vzorce dosadíme místo hodnoty M = 29 kg/kmol hodnotu molární hmotnosti vypočtenou ze složení (ve spalinách a vzdušině se jedná o složky: O2, CO2, H2O a N2) dle vztahu (16), pak lze přepsat vztah (14) na základní vztah (17).
kde je
- φi
- – objemový zlomek i-té složky,
- Mi
- – molární hmotnost i-té složky v kg/kmol.
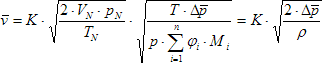 (17)
[m/s]
(17)
[m/s]
Průtok za podmínek měření (efektivní podmínky) lze vypočítat dle vztahu:
K přepočtu na normální podmínky lze použít vztah:
Pomocná zařízení
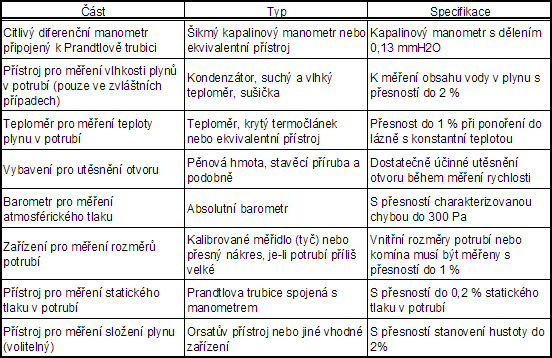
Požadavky na pomocná zařízení pro měření Prandtlovou trubicí jsou shrnuty v tab. č. 6.
Tab. č. 6 Pomocná zařízení a jejich specifikace
Přesnost
Norma je koncipovaná jako doporučení a uvádí, že pokud budou splněny požadavky v ní uvedené, bude výsledná chyba spojená s měřením rychlosti v potrubích menší než 3 %.
V jiných případech má být menší než 5 %. Přítomnost tuhých částic a aerosolů, které mohou ucpat otvory Prandtlovy trubice, může chybu zvyšovat. Zvýšení počtu vzorkovacích bodů může přesnost lehce zvýšit, ale při překročení šestnácti bodů je dosažené snížení chyby velmi malé. Zvýšení přesnosti, které však nepřekračuje 5 %, může být dosaženo správným určením složení, hustoty a obsahu vlhkosti.
Druhá část článku, která bude následovat, obsahuje příklad výpočtu rychlosti a průtoku, a dále kapitoly 3. Tlak a jeho stanovení, 4. Teplota a její stanovení, 5. Závěr.
The paper is focused on the problem of measurement of gas flow in closed conduits. It deals with the physical principles of measurement and refers to standardized procedures which deal with this issue. It is also briefly discussed the measurement of temperatures and pressures as these parameters are important for calculations of flow.