Vzpěrné délky ocelových oblouků. Část 2: Trojkloubové oblouky
V Části 2 jsou uvedeny vzpěrné délky týkající se oblouků trojkloubových, a to jak s vrcholovým kloubem vidlicovým (pouze v rovině oblouku), tak i trojkloubových oblouků s vrcholovým kloubem úplným (v rovině i z roviny oblouku). Článek navazuje na Část 1 [1], která zahrnuje oblouky dvojkloubové a vetknuté. Všechny studie jsou provedeny pro tři typy rovnoměrného zatížení (svislé po délce oblouku, svislé na půdorys oblouku a zatížení radiální). Hodnoty vzpěrných délek ekvivalentního přímého (Eulerova) prutu s konstantní osovou silou odpovídající maximální osové síle v patce oblouků jsou uvedeny ve formě grafů pro uzavřené trubkové průřezy, pro různé otevřené válcované průřezy IPE a různé širokopřírubové průřezy HEB.
Část 1: Dvojkloubové a vetknuté oblouky
1. Úvod
Stabilitní studie trojkloubových oblouků a odtud vyplývající součinitele vzpěrných délek vychází ze stejných předpokladů uvedených v Části 1 [1]. Týká se trojkloubových oblouků s vidlicovým i úplným vrcholovým kloubem, pro tři typy zatížení, 7 různých průřezů a pět poměrů H/L (vzepětí k půdorysné délce oblouku). Pro rovnoměrná zatížení a odpovídající proměnnou osovou sílu oblouku jsou vzpěrné délky vždy vztaženy k maximální osové síle v patě oblouku, která vstupuje do posouzení ekvivalentního základního (Eulerova) prutu daného průřezu.
Podobně jako v Části 1 platí, že vzpěrná délka oblouku scr je vztažena k celé délce oblouku (s) jak pro vybočení v rovině, tak i z roviny oblouku (oproti např. mostní normě ČSN EN 1993-2/2007, kde pro vybočení v rovině oblouku je součinitel vzpěrné délky vztažen k poloviční délce oblouku s/2 a pro vybočení z roviny oblouku k celé půdorysné délce L. Přepočet na jiné vztažné délky lze provést jednoduchým přenásobením poměrem vztažných délek (viz [1]).
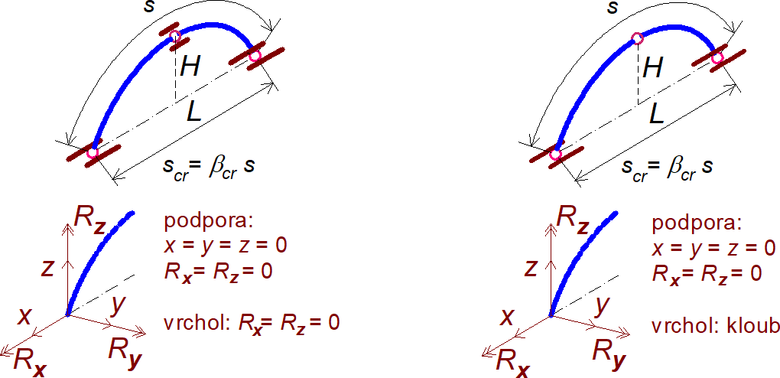
Okrajové podmínky pro trojkloubové oblouky jsou uvedeny na obr. 1. Podobně jako v Části 1 je v podporách uvažováno kloubové vidlicové (čepové) uložení. Ve vrcholovém kloubu oblouku je variantně zavedeno obdobné vidlicové uspořádání (vetknutí z roviny oblouku), nebo úplný kloub (i pro vybočení z roviny oblouku). Pro kritická zatížení oblouků byla opět použita 3D LBA v programu SCIA Engineer (verze 20.0). Parametrická studie zahrnuje základní geometrii s vidlicovým uložením podle obr. 1 (L = 10 m, 125 uzlů na oblouku, 6° volnosti, přímý řešič LanCZOS, 50 vlastních tvarů).
Opět se připomíná, že volně stojící oblouky jsou spíše výjimečné, neboť pro příčné zatížení musí být náležitě dimenzovány (jako „balkonové oblouky“) a obvykle jsou proto příčně ztuženy (uváděné vzpěrné délky pro vybočení z roviny se neuplatní).
2. Zásady pro stanovení vzpěrných délek oblouků
Pro stanovení součinitele vzpěrné délky oblouku s proměnnou osovou silou se postupuje stejně jako v Části 1, tzn., že platí:
kde se podle tvarů vybočení trojkloubových oblouků uplatní převodní součinitele:
- pro vybočení v rovině oblouků (dvě sinusové polovlny nebo prolomení ve vrcholu) součinitel δT,
- pro vybočení z roviny oblouku (vetknutí v patě oblouku) součinitel δD.
Z analýzy oblouků ve 3D byla získána kritická zatížení pro vybočení v rovině (Ncr,y) i z roviny oblouků (Ncr,z). Pro součinitel vzpěrné délky převádějící kritické zatížení oblouku s danou proměnnou osovou silou Ncr na Eulerův prut s konstantní osovou silou je opět vybrán průřez v patě oblouku, s osovou silou Nmax.
3. Parametrická studie trojkloubových oblouků
Kritická zatížení a vzpěrné délky oblouků byly řešeny pro 5 vztažných poměrů vzepětí k výšce oblouku: H/L ∈ < 0,1; 0,5 >. Kritická zatížení oblouků ve 3D jsou závislá na poměrech tuhostních parametrů průřezu oblouku. Pro vybrané uzavřené průřezy (všechny kruhové trubky) a otevřené válcované průřezy IPE a HEB jsou tyto parametry uvedeny v Části 1, Tab. 1.
4. Vzpěrné délky trojkloubových oblouků s vidlicovým vrcholovým kloubem (vztažené k osové síle v patě Nmax)
4.1 Zatížení po délce oblouku
4.1.1 Trubky a otevřené průřezy „na stojato“
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 2. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 2. Hodnota Nmin pro δT je stanovena v s/2 a pro δD v s/4.
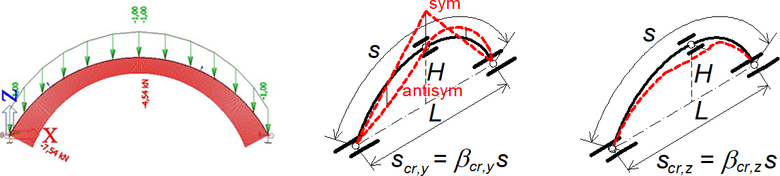
Obr. 2 Příklad trojkloubového oblouku s vidlicovým vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,837 | 0,866 | 0,902 | 0,943 | 0,983 |
| √δD | 0,884 | 0,904 | 0,929 | 0,959 | 0,987 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 3.
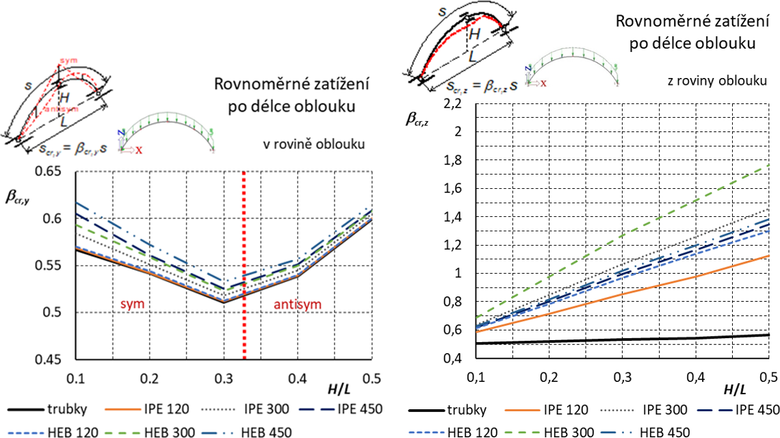
Obr. 3 Trojkloubový oblouk s vidlicovým vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
4.1.2 Trubky a otevřené průřezy „na ležato“
Obdobně jako v Části 1 rozhoduje o součinitelích vzpěrných délek poměr momentu setrvačnosti k momentu v prostém kroucení (Iz /IT). U otevřených průřezů tedy rozhoduje poloha průřezu (viz Tab. 1 [1]). Hodnoty vzpěrných délek pro průřezy orientované „na ležato“ jsou uvedeny na obr. 4. Podobně jako u dvojkloubových a vetknutých oblouků je zřejmé, že součinitele pro vybočení v rovině oblouku nyní splývají se součiniteli pro trubky, pro vybočení z roviny jsou však ve srovnání se součiniteli vzpěrných délek pro průřezy orientovanými „na stojato“ mnohem vyšší. Pro další typy zatížení dvojkloubových oblouků je situace obdobná a poloha „na ležato“ není uváděna.
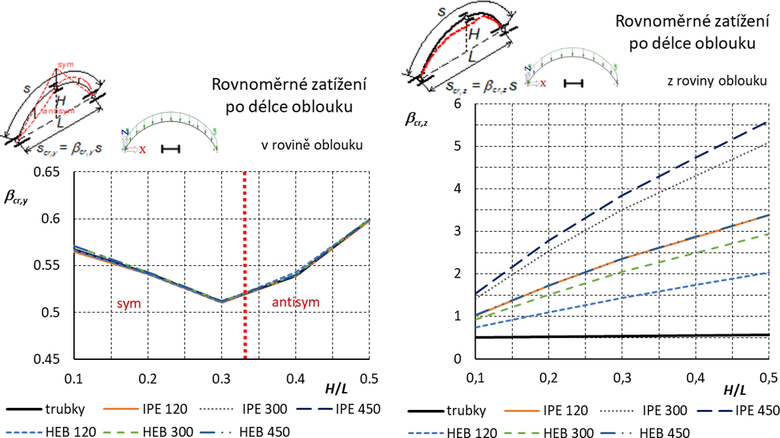
Obr. 4 Trojkloubový oblouk s vidlicovým vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na ležato“
4.2 Zatížení na půdorys oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 5. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 3. Hodnota Nmin pro δT je stanovena v s/2 a pro δD v s/4.
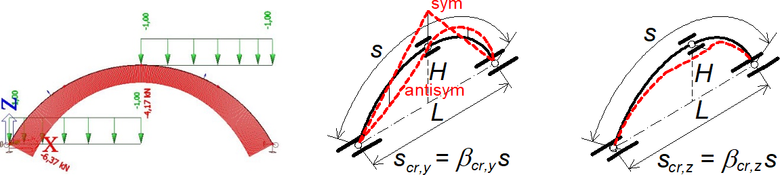
Obr. 5 Příklad trojkloubového oblouku s vidlicovým vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,867 | 0,890 | 0,915 | 0,948 | 0,983 |
| √δD | 0,905 | 0,921 | 0,938 | 0,962 | 0,988 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 6.
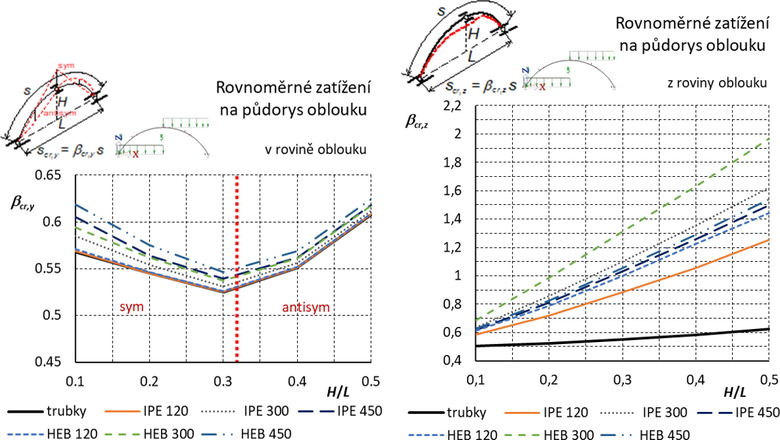
Obr. 6 Trojkloubový oblouk s vidlicovým vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku
4.3 Radiální zatížení oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 7. Protože osová síla v oblouku je konstantní, pro převodní součinitele platí δT = δD = 1.
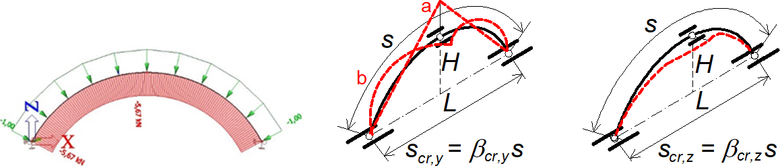
Obr. 7 Příklad trojkloubového oblouku s vidlicovým vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 8. Pro vysoké oblouky (H/L → 0,5) může být kritická deformace při vybočení v rovině oblouku dvojího typu, jak ukazuje obr. 7.
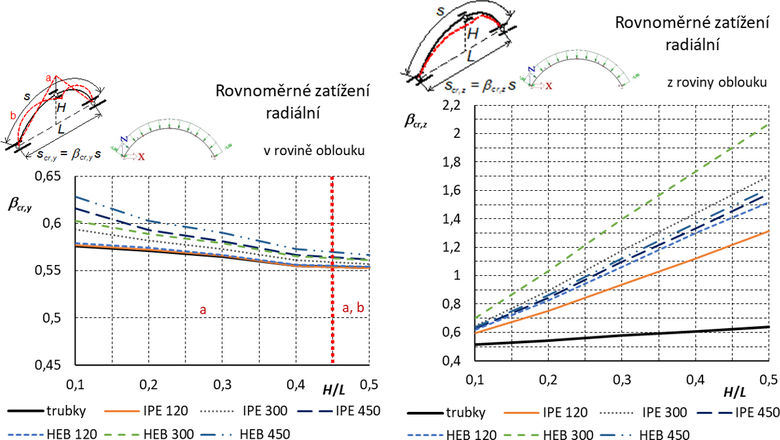
Obr. 8 Trojkloubový oblouk s vidlicovým vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku
5. Vzpěrné délky trojkloubových oblouků s úplným vrcholovým kloubem (vztažené k osové síle v patě Nmax)
5.1 Zatížení po délce oblouku
5.1.1 Trubky a otevřené průřezy „na stojato“
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 9. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 4. Hodnota Nmin pro δT je stanovena v s/2 a pro δD rovněž v s/2.
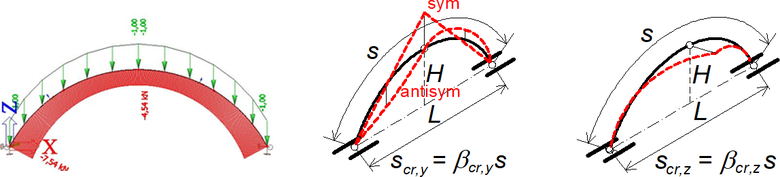
Obr. 9 Příklad trojkloubového oblouku s úplným vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,837 | 0,866 | 0,902 | 0,943 | 0,983 |
| √δD | 0,751 | 0,797 | 0,853 | 0,916 | 0,975 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 10.
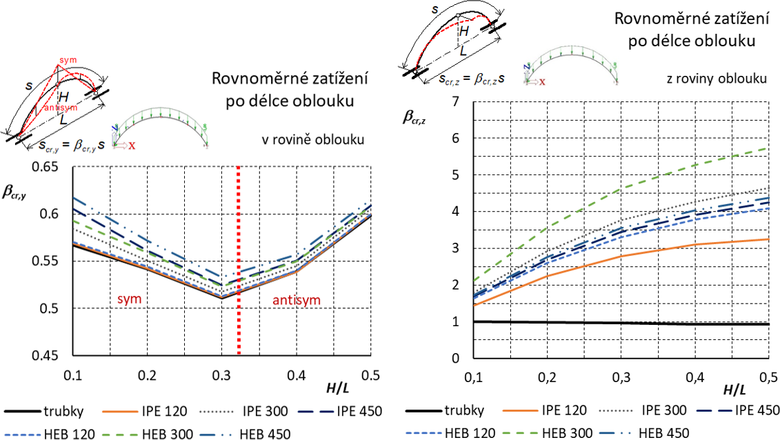
Obr. 10 Trojkloubový oblouk s úplným vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na stojato“
5.1.2 Trubky a otevřené průřezy „na ležato“
Vliv polohy průřezu je pro otevřené průřezy opět významný. Hodnoty vzpěrných délek pro otevřené průřezy orientované „na ležato“ (s výrazně vyššími poměry momentu setrvačnosti k momentu v prostém kroucení, viz Tab. 1 [1]), jsou uvedeny na obr. 11. Stejně jako u trojkloubových oblouků s vidlicovým vrcholovým kloubem součinitele pro vybočení v rovině oblouku splývají se součiniteli pro trubky, pro vybočení z roviny jsou však ve srovnání se součiniteli vzpěrných délek pro průřezy orientovanými „na stojato“ mnohem vyšší. Pro další typy zatížení dvojkloubových oblouků je situace obdobná a poloha „na ležato“ již není uváděna.
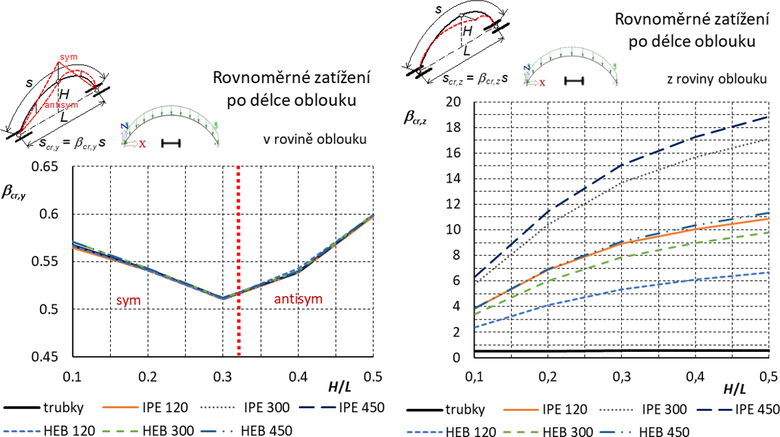
Obr. 11 Trojkloubový oblouk s úplným vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku. Otevřené průřezy jsou orientovány „na ležato“
5.2 Zatížení na půdorys oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 12. Podle tvaru vybočení jsou převodní součinitele náležející Nmax pro vybočení v rovině oblouku (δT) a z roviny oblouku (δD) uvedeny v Tab. 5. Hodnota Nmin pro δT je stanovena v s/2 a pro δD rovněž v s/2.
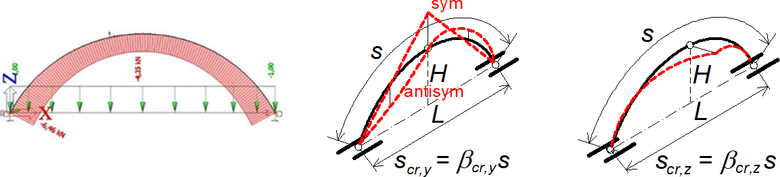
Obr. 12 Příklad trojkloubového oblouku s úplným vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
| H/L | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
|---|---|---|---|---|---|
| √δT | 0,992 | 0,976 | 0,962 | 0,952 | 0,944 |
| √δD | 0,987 | 0,963 | 0,943 | 0,928 | 0,914 |
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 13.
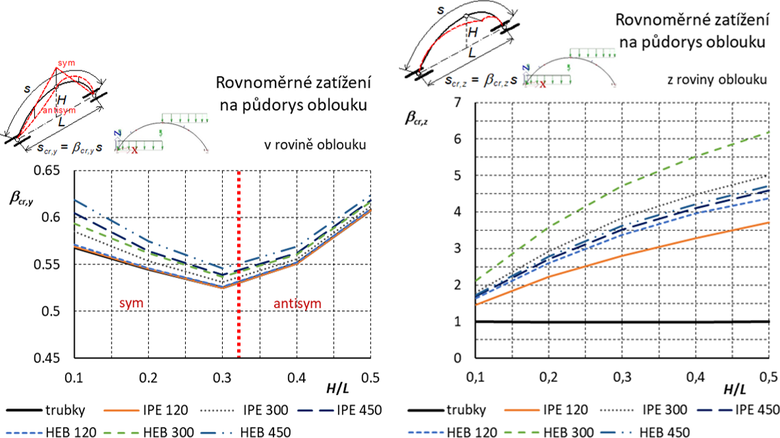
Obr. 13 Trojkloubový oblouk s úplným vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku
5.3 Radiální zatížení oblouku
Příklad oblouku, zatížení a vybočení v rovině i z roviny oblouku je na obr. 14. Protože osová síla v oblouku je konstantní, pro převodní součinitele platí δT = δD = 1.
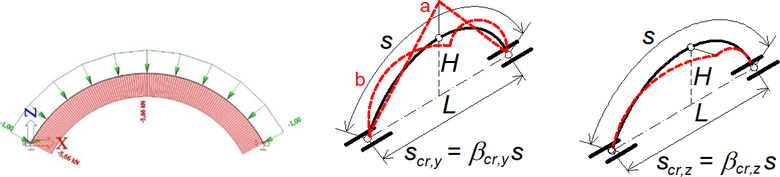
Obr. 14 Příklad trojkloubového oblouku s úplným vrcholovým kloubem a poměrem H/L = 0,3. Vybočení v rovině a z roviny oblouku
Výsledné grafy pro součinitele vzpěrných délek jsou uvedeny na obr. 15.
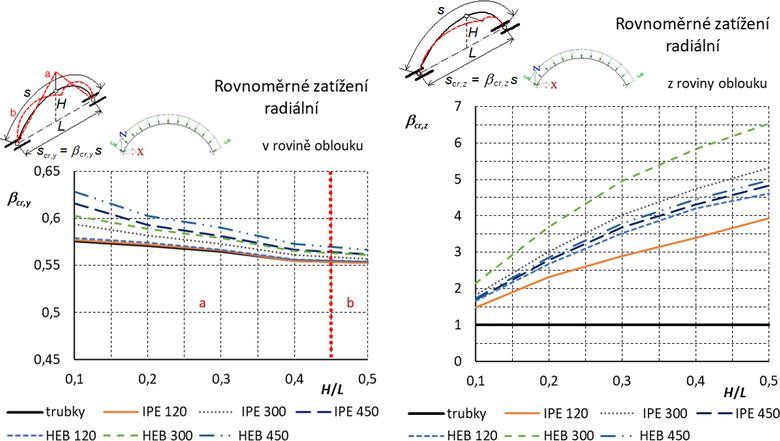
Obr. 15 Trojkloubový oblouk s úplným vrcholovým kloubem: Součinitele vzpěrných délek pro vybočení v rovině a z roviny oblouku
6. Závěr 2. části
Uvedené křivky součinitelů vzpěrných délek trojkloubových oblouků s vidlicovým a úplným vrcholovým kloubem jsou vztaženy k osové síle v patě oblouků (Nmax) a vedou k následujícím závěrům:
- Vliv konstrukce vrcholového kloubu (vidlicový nebo úplný) se projeví pouze pro součinitele vzpěrných délek pro vybočení z roviny oblouků a je podstatný. Zatímco pro vidlicový vrcholový kloub je tvar vybočení z roviny oblouku ve vrcholu hladký, pro úplný kloub dochází k prolomení.
- Kritický tvar pro vybočení v rovině trojkloubových oblouků je pro ploché oblouky symetrický (prolomením), pro vysoké oblouky antisymetrický. Vliv tvaru průřezu na součinitele vzpěrných délek je malý.
- Vliv tvaru průřezu (uzavřené trubky, otevřené IPE a HEB) je naopak velmi výrazný pro součinitele vzpěrných délek při vybočení z roviny oblouku. Z analýzy křivek vzpěrných délek a Tab. 1 [1] plyne, že rozhodujícím parametrem je podíl tuhosti k netuhé ose pro vybočení z roviny oblouku a tuhosti v prostém kroucení (Iz /IT). U profilů IPE a HEB lze provádět interpolaci hodnot pod a nad hraničními průřezy IPE300 a HEB300.
- Součinitele vzpěrných délek jsou lineárně závislé na vztažné délce, v této studii je jí délka oblouku s. Pro jiné vztažné délky (např. s/2 nebo L, jak je tomu např. v Eurokódu ČSN EN 1993-2) lze tedy provést jednoduché přenásobení poměrem vztažných délek. V této souvislosti lze upozornit, že hodnoty vzpěrných délek v běžných normách (a též v ČSN EN 1993-2) platí pouze pro uzavřené průřezy (trubky) a nezahrnují korekci na vliv proměnné síly v oblouku. Ze studie rovněž plyne, že kritické tvary vybočení pro případné řešení geometricky nelineární analýzou (GNIA), popř. zjednodušenou teorií 2. řádu, jsou závislé na okrajových podmínkách. Pro trojkloubové oblouky s běžným vidlicovým uložením v podporách není pro tvar vybočení z roviny oblouků vliv příslušného vetknutí v normách předpokládán.
7. Literatura
- Macháček, J.: Vzpěrné délky ocelových oblouků. Část 1: Dvojkloubové a vetknuté oblouky. TZB-info, ocelové konstrukce, 2022, 12 s.
Poděkování
Článek a související výzkum vznikl za podpory grantu ČVUT SGS22/141/OHK1/3T/11.
Part 2 covers buckling lengths of three-hinged arches both with the crown hinge of a fork type (in the arch plane) and a full type (both in and out of the arch plane). The article follows the Part 1 [1] which deals with two-hinged and built-in arches. All studies present three uniform loading patterns (vertical along the arch length, vertical to the arch plan or radial to the arch axis). Buckling lengths of the equivalent straight (Euler’s) column with the constant axial force corresponding to maximal axial arch force in the arch bases are presented in the form of graphs for CHS (circular hollow sections), various open rolled IPE and HEB sections.