Prognóza tepelného chování půdní vestavby pro návrh klimatizace

Vzhledem k tomu, že cílem výzkumného záměru je určitá prefabrikace navržených systémů, tj. výstupem bude určitá katalogová nabídka různých modifikací systémů techniky prostředí, včetně zhodnocení po stránce energetické, ekonomické i vytvořeného uživatelského komfortu, je nutná poměrně přesná prognóza tepelného chování prostoru. Za tímto účelem autoři používají vlastní software Teruna. Příspěvek bude věnován idealizacím výpočtového modelu, jeho struktuře a mechanismu výpočtu, hodnocení výsledků, experimentálnímu ověření modelu měřením v reálné půdě a následně možností integrace chladivového klimatizačního systému do půdní vestavby.

METODA ŘEŠENÍ

Jako výchozí byl přijat model budovy jako otevřené termodynamické soustavy s nestacionárním chováním. Tepelné děje, které v ní probíhají lze popsat diferenciálními rovnicemi, které po doplnění okrajových podmínek vytvoří matematický model úlohy. Diferenciální úloha je nahrazena úlohou diferenční na základě diskretizace v čase a prostoru. Vstupní i výstupní veličiny tedy mají diskrétní charakter.

Pro tuto úlohu byl vytvořen matematický model, který představuje systém relevantních prvků a veličin a jejich vzájemných vazeb na základě vlastností reálného objektu. Z analýzy tepelných bilancí běžných budov vyplývají jako podstatné pro vstup do matematického modelu následující prvky a charakteristické způsoby přenosu tepla uvedené v tabulce 1. Názvy jednotlivých prvků je nutno chápat symbolicky jako typického představitele určité stavební konstrukce nebo vybavení budovy s konkrétními vlastnostmi a postavením v tepelné bilanci. Základní jednotkou pro řešení je jedna místnost, příp. zóna s jednou teplotou vzduchu.

Model je jednorozměrný, jednotlivé prvky jsou nahrazeny hmotnými body. Jedním z bodů je také vnitřní vzduch. Tepelné vazby mezi prvky udávající vzájemnou interakci jsou pro vybranou úlohu znázorněny na obr. 2.

Tepelně technické vlastnosti materiálů a hmot se uvažují jako konstantní a izotropní a mají nekonečný difúzní odpor. Tepelný tok stěnou se uvažuje jednorozměrný. Součinitelé přestupu tepla sáláním a konvekcí u jednotlivých prvků se uvažují konstantní hodnotou. Krok časové diskretizace je volitelný od 10 do 3600s. Čas ve výpočtu je shodný se slunečním časem.

Na základě uvedených předpokladů a výpočtových formulí byl sestaven výpočtový program TeRuNa. Tento program umožňuje řešení obou základních úloh (tepelného chování a tepelné ztráty/zátěže místnosti). Krok časové diskretizace je volitelný 10 - 7200 s a pro tento krok lze výpočet realizovat v cyklu 1-360 dnů, podle zjednodušeného kalendáře vytvořeného 12 měsíci po 30 dnech. Do výpočtu může vstoupit 16 hlavních prvků (W, V, St, Po - tvoří hranici místnosti) a mnoho dalších (Bi, Vo, Sp, Ak, Ve, Os, Sv - vyjadřují vnitřní zdroje).

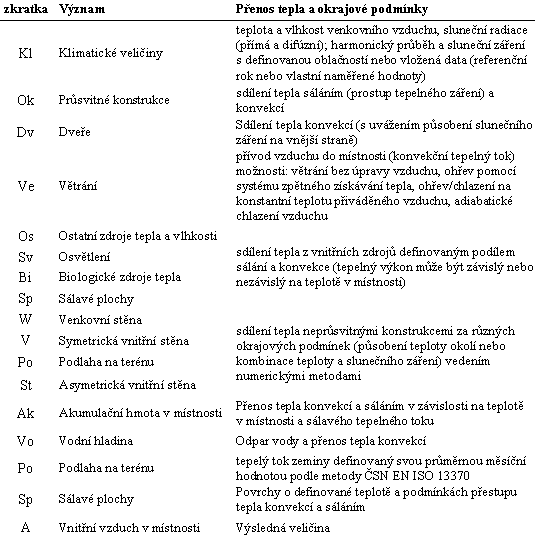
Tab. 1 Prvky matematického modelu a pro ně definovaný způsob přenosu tepla a okrajové podmínky tepelné bilance

Matematický model má pro praktické řešení podobu výpočtového modelu realizovaného jako počítačový software. Z hlediska programového řešení se jedná o program napsaný v object pascalu, přesněji v programovacím jazyku Delphi. Program je optimalizovaný pro Windows 2000/XP při rozlišení 1024x768 s 16 bitovou barevnou hloubkou. Doporučená konfigurace počítače je Intel Celeron 300MHz, 150MB HDD, 128MB RAM. Jsou zde implementovány rutiny vytvořené ve strojovém kódu, které výrazně urychlují výpočet náročnějších matematických funkcí. Je využíváno dynamického alokování proměnných umožňující snížení náročnosti na velikost operační paměti. Využití operační paměti se pohybuje, v závislosti na náročnosti a přesnosti výpočtu, od 5MB do 96MB RAM. Program ukládá za chodu vypočítaná data do adresáře /CACHE, kde mohou zabírat až 100MB místa na disku. Pokud dojde k neočekávanému ukončení s nutností restartování systému, adresář CACHE zůstává zachován a později, při novém spuštění, je opětovně využit, což ve většině případů zamezí ztrátě dat. Uživatelské prostředí je vytvořeno na principu roletového menu s otevíráním jednotlivých oken pro zadávání, výpočet a zobrazení výsledků, které umožňuje aktivní přepínání mezi zadáváním hodnot, výpočtem a zobrazováním výsledků. Veškeré vstupní hodnoty lze buď jednotlivě nebo jako celek uložit na disk a je možné se k nim později vrátit. Program bude obsahuje aktivní Help, kdy se v okně zobrazuje pomocný text v závislosti na aktuální pozici.

Obr. 1 - Ukázka prostředí programu Teruna

Program je uspořádán tak, aby svým prostředím a nároky na potřebné znalosti byl přístupný i uživatelům z řad širší odborné veřejnosti (obr. 1).

STUDIE TEPELNÉHO CHOVÁNÍ PŮDNÍ VESTAVBY

Stěžejním cílem výzkumného záměru je unifikace a následná prefabrikace prvků stavby i systémů TZB, přičemž se předpokládá integrace mnohých součástí systémů do stavebních konstrukcí, zejména solárních kolektorů (vzduchových i kapalinových) nebo částí potrubní sítě pro vedení teplonosných látek. Vzhledem k široké rozměrové paletě střech, na které lze střešní nástavby instalovat, je nutno hledat přijatelná zjednodušení konkrétních parametrů stavby tak, aby bylo možno uplatnit jedno vzorové (typizované) řešení na větší počet stavebních objektů. Jednou z okolností, kterou novou střešní nástavbou nebo vestavbou lze jen minimálně ovlivnit, je tvar střechy, její sklon a orientace ke světovým stranám. Sklon střešní roviny v rozpětí 35° až 45° bude mít zřejmě minimální dopad, proto bude v dalším věnována pozornost vlivu orientace ke světovým stranám.

Matematický model úlohy využívá možností programu Teruna. Relevantní prvky a jejich vazby jsou znázorněny na obr. 2. Krátkovlnné sálání od Slunce prochází průsvitnými částmi obálky místnosti a je rozděleno na jednotlivé plochy v místnosti. Ty předávají teplo pouze konvekcí, dlouhovlnné sálání je zanedbáno, resp. ošetřeno zvýšením přestupu tepla konvekcí. Testovací úlohy prokázaly, že tato úprava, výrazně zjednodušující řešení úlohy i zadávání geometrie prostoru, nemá v běžných případech podstatný vliv na výsledek.

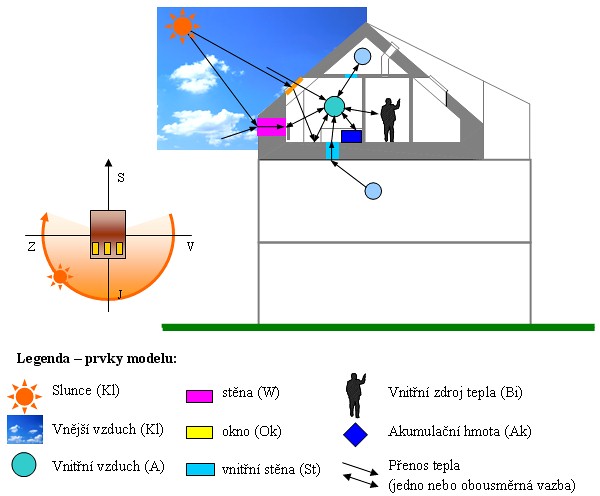
Obr. 2 Schéma prvků matematického modelu a vzájemné tepelné vazby, orientace ke světovým stranám

Pro variantní výpočty byly přijaty následující podmínky:

• Jednorozměrný tepelný model, teplota vnitřního vzduchu nahrazena jednou průměrnou hodnotou
• rozměry místnosti 3x5x2,5 m, sklon střešní roviny 40°
• šikmá střecha s keramickou krytinou zateplená izolací tl. 250 mm s tepelnou vodivostí 0,04 W/mK
• obvodové zdivo keramické tl. 300 mm, zateplené izolací tl. 100 mm s tepelnou vodivostí 0,04 W/mK
• Pohltivost sluneční radiace střešním pláštěm 0,8
• 3 okna o rozměrech 0,8x1,4 m, U = 1,1 W/m²K, stínící součinitel s = 0,5
• Orientace šikmou střešní rovinou s oknem k jihu nebo západu
• Klimatické podmínky jako výpočtové extrémy pro letní období; teplota vnějšího vzduchu hladkým průběhem s harmonickým kolísáním s maximem 30 °C v 15 h a nejnižší teplotou 20 °C v 3 h (odpovídá trendu teploty v městské zástavbě, kdy v důsledku tepelné akumulace staveb teplota v noci neklesá na dříve uvažovanou hodnotu 16°C)
• teplota v půdním prostoru (nad obytným) jako venkovní zvýšená o 5 K
• Zeměpisná poloha ČR - 50° s.š., 17° z.d.
• Průvzdušnost a větrání způsobují trvalou výměnu vzduchu 0,5 /h, větrání otevřenými okny dosahuje výměny vzduchu 2 /h.
• Vnitřní zdroje tvoří 2 osoby
• Vnitřní zařízení sloužící pro akumulaci tepla o hmotnosti 100 kg

Výsledky

V následujících obrázcích jsou shrnuty výsledky počítačových experimentů, jejichž cílem je porovnat vliv různých okrajových podmínek daných orientací ke světovým stranám. Jako kritérium byla použita maximální dosažená teplota vzduchu v místnosti a čas jejího dosažení reprezentující tepelnou setrvačnost. Výsledky jsou zobrazeny v tab. 2. Jak je patrné z výsled-ných hodnot, s uvážením vlivu akumulace, který umožňuje výpočtový model, jsou rozdíly zcela zanedbatelné. Při orientaci oken na sever je dosahováno cca 75% hodnoty maximální tepelné zátěže. Rozdíl je tedy z hlediska dimenzování prvků zanedbatelný. Rozdílný bude samozřejmě průběh tepelné zátěže během dne, který však na volbu velikosti zařízení v tomto případě nemá vliv. Z hlediska dopadající sluneční radiace je nejméně příznivá orientace k jihozápadu, kde sluneční paprsek svírá ve 14 h slunečního času s normálou střešní roviny úhel menší jak 10°. Dominantní podíl na tepelné zátěže má tedy prostup sluneční radiací (stí-nící součinitel okna 0,5) - pro JZ stěnu je to 76 %, dále lidé 12 %, větrání 6%, prostup neprů-svitnými konstrukcemi méně jak 4 %.

Světová strana	Maximální teplota	čas	Maximální tepelná zátěž	čas
V	41,7	13:30	1090	12:25
JV	42,8	13:35	1138	13:15
J	42,9	15:20	1147	14:00
JZ	42,5	15:55	1131	14:15
Z	41,7	16:10	1104	14:30

Tab. 2 Maximální teplota vzduchu v místnosti bez klimatizace, čas jejího dosažení,
max. hodnota tepelné zátěže pro udržení vnitřní teploty vzduchu 26°C

Dosažené výsledky nejsou průlomem ve výpočtech tepelných bilancí a nepopírají základní známou skutečnost, že poloha průsvitných konstrukcí vůči Slunci má zásadní vliv na hodnotu dopadajícího slunečního záření. Poloha Slunce na obloze je osově symetrická podle osy S-J, maximální radiace je dosažena v odlišnou dobu, na jižní straně je ve svislé stěně radiace nižší, v případě šikmé roviny je tento vliv kompenzován výhodnou polohou stěny vůči slunečnímu paprsku. Šikmá střešní rovina je osluněna téměř celodenně a neplatí pro ni závěry pro stěny svislé. Tato skutečnost je také podpořena tvarem střešních oken, která nemají ostění vytvářející stíny, jak je běžné u svislých stěn s okny.

Zásadním prvkem v tepelné bilanci je tedy okno; maximum tepelné zátěže pro JZ orientaci se při změně součinitele prostupu tepla změní málo (pro U = 1,1 W/m²K je Q = 1131 W; pro U = 0,7 W/m²K je Q = 1126 W, maximální teplota však vzroste ze t = 42,5 °C na t = 43,0 °C, neboť se sníží ztráta konvekcí v noci). Větší význam má volba stínícího součinitele. Základní hodnota s = 0,5 předpokládá běžně dosažitelné stínící prostředky, které jsou používány i pro zvýšení zrakové pohody. Nestíněné okno zdvojené lze aproximovat s = 0,85, pro které Q = 1700 W.

EXPERIMENTÁLNÍ OVĚŘENÍ - NEZATEPLENÝ PŮDNÍ PROSTOR

Aby mohla být posouzena správnost dosažených výsledků, bylo přikročeno také k experimentálnímu ověření modelu v reálné budově. K tomu účelu byl vybrán nezateplený půdní prostor v obytném domě. Venkovní stěna je tak vytvořena pouze keramickými taškami na laťování, má tedy minimální tepelný odpor, útlum a setrvačnost. Kolísání venkovní teploty a sluneční radiace se výrazně projeví na průběhu teploty vnitřního vzduchu i na teplotách povrchů tašky a vnitřních stěn. Vnitřní stěna odděluje prostor půdy od zatepleného podkroví a podlaha od nižších podlaží bytů. Zjednodušené schéma je na obr. 4. Pro porovnání byl vybrán den s převážně jasnou oblohou. Grafické zpracování výsledků jen na obr. 5 a 6.

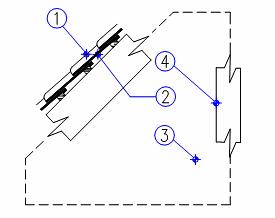
Obr. 4 Zjednodušené schéma půdního prostoru pod sedlovou střechou s jednoduchou keramickou
krytinou na laťování na dřevěném krovu. Čísly jsou označeny měřené teploty vynesené v grafech.

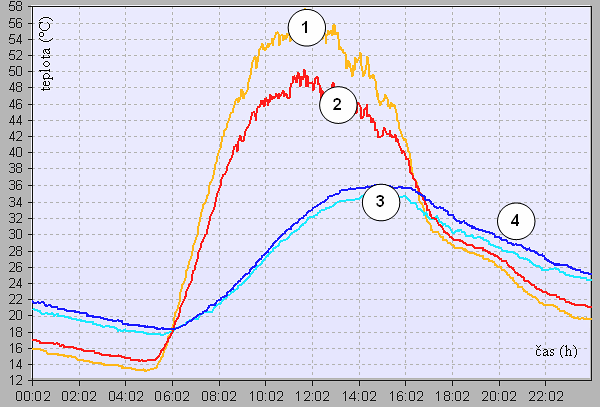
Průběh teplotních veličin získaný simulací je velmi blízký průběhu získaného měřením. Rozdíl mezi naměřenou a vypočtenou hodnotou povrchové teploty tašek z vnitřní a vnější strany vykazuje max. odchylku 2 K, rozdíl u teploty vzduchu a povrchů nepřesahuje 1 K. Povrchová teplota keramické krytiny však vzhledem k minimální tloušťce, akumulaci a tepelnému odporu vykazuje silnou závislost na součinitelích přestupu tepla, jejichž hodnota je v modelu určena pouze konstantou. Z tohoto pohledu je tedy úloha tepelného chování místnosti se subtilními stěnami špatně podmíněná oproti úlohám s robustními stěnami.

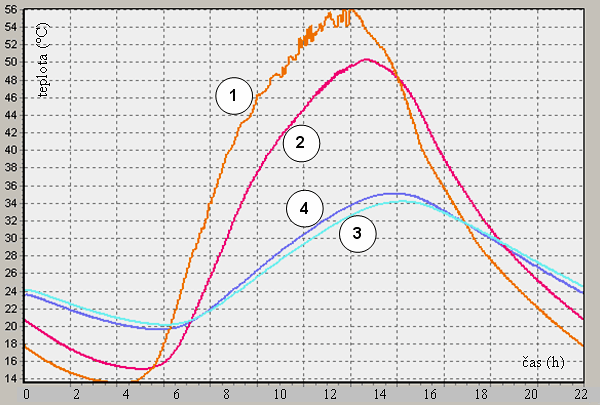
Obr. 6 - Vypočtený průběh teploty v půdním prostoru v červnu při jasné obloze

Výsledky experimentu dokladují správnost matematického modelu i jeho výpočtové softwarové formy.

ZÁVĚR

Experimentální cestou bylo prokázáno, že matematický model implementovaný v programu Teruna je vhodným nástrojem pro řešení úloh tepelné bilance a prognózy tepelného chování místnosti. Výsledky případové studie ukazují, že u šikmých střech, které jsou v letním období kdy je Slunce vysoko nad obzorem osluněny téměř po celý den, nemá orientace ke světovým stranám zásadní dopad na maximální hodnotu tepelné zátěže a vzorový pokoj se třemi střešními okny lze orientovat s azimutem stěny 90° až 180° bez změny výkonu klimatizačního zařízení. To je předpokladem unifikace použitých prvků ve střešních nástavbách, příklad uvádí obr. 7.

V prostoru krovu bude tvar střechy upraven pro instalaci venkovní jednotky klimatizačního zařízení. Vzhledem k jednotné velikosti zařízení bude možno optimalizovat střešní dílec z hlediska velikosti, akustickým vlastnostem z hlediska šíření hluku od jednotky do venkov-ního prostoru i z hlediska přenosu vibrací.

LITERATURA

[1] Rubinová O., Počinková M., Hirš J.: Střešní nástavby - místo pro bydlení, Topenářství a instalace 6/2007

Tento text byl zpracován s podporou výzkumného záměru IEA BCS Annex 50 - Prefabrikace systémů pro nízkoenergetickou renovaci obytných budov