Stanovení účinnosti plochého solárního kolektoru (II)
Pro stanovení účinnosti plochého solárního kolektoru nejsou v žádné naší literatuře ucelené analytické a experimentální vztahy. Seriál tří článků uvádí stručný rozbor a definuje základní vztahy k této problematice. Druhý díl je zaměřen na vnitřní energetickou bilanci absorbéru.
VNITŘNÍ ENERGETICKÁ BILANCE ABSORBÉRU
Fyzikální procesy odehrávající se v absorbérech plochých solárních kolektorů je možné teoreticky popsat vnitřní energetickou bilancí, vyjadřující přenos tepla z povrchu absorbéru do teplonosné látky. Konstrukce plochých kolektorů je zpravidla založena na trubce protékané teplonosnou látkou, na které je připevněna lamela s povrchem určeným k absorpci slunečního záření. Základem teoretického řešení tepelného chování absorbéru je výpočet teplotního pole na lamele (technicky známého žebra s dopadem slunečního záření), tedy diferenciální rovnice druhého řádu se dvěma okrajovými podmínkami, a řešení teplotního pole na trubce.
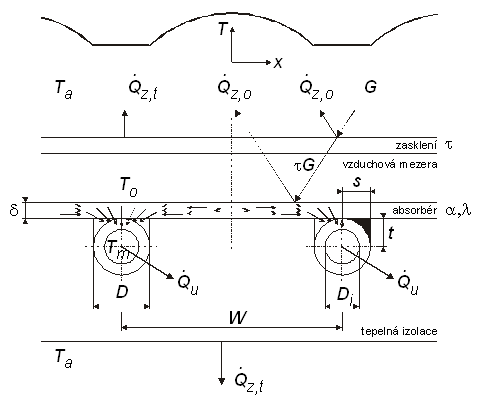
Obr. 3 - Znázornění bilance vně a uvnitř absorbéru a průběhu teplot v lamele
Částečným výsledkem řešení je tepelný tok lamelou (žebrem) k trubce, vztažený na jednotku délky trubky
| (5) |
kde F (-) je standardní účinnost žebra daná vztahem
| (6) |
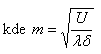 | (7) |
a tepelný tok (zisk) trubky samotné, vztažený na jednotku délky
| (8) |
Využitelný tepelný tok ![]() (W/m) musí být přenesen z povrchu lamely a trubky do teplonosné látky (kapaliny) proudící uvnitř trubky. Odpor proti toku tepla do kapaliny je dán tepelným odporem spoje lamely s trubkou a tepelným odporem proti přestupu tepla z vnitřního povrchu trubky do kapaliny. Využitelný tepelný tok je pak dán rovnicí
(W/m) musí být přenesen z povrchu lamely a trubky do teplonosné látky (kapaliny) proudící uvnitř trubky. Odpor proti toku tepla do kapaliny je dán tepelným odporem spoje lamely s trubkou a tepelným odporem proti přestupu tepla z vnitřního povrchu trubky do kapaliny. Využitelný tepelný tok je pak dán rovnicí
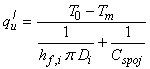 | (9) |
kde Di (m) je vnitřní průměr trubky, hf,i (W/m2K) je součinitel přestupu tepla mezi vnitřním povrchem trubky a teplonosnou látkou. Teplota T0 (°C) je teplota v patě lamely (žebra) a teplota Tm (°C) je střední teplota teplonosné látky v trubce daná aritmetickým průměrem
| (10) |
kde Tin (°C) je teplota na vstupu do kolektoru a Te (°C) je teplota na výstupu z kolektoru.
Tepelná propustnost spoje Cspoj (W/mK) je odhadnuta na základě známé tepelné vodivosti spoje λspoj (W/mK), průměrné tloušťky spoje t (mm) a šířky spoje s (mm) (viz obr. 3) a je vztažena na jednotku délky trubky
| (11) |
Eliminací teploty v patě lamely T0 z rovnic je možné vyjádřit využitelný tepelný tok na základě parametrů kolektoru (rozměrů, fyzikálních vlastností) a teploty teplonosné látky
| (12) |
kde F' (-) je účinnostní součinitel kolektoru
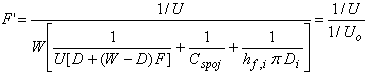 | (13) |
Účinnostní součinitel kolektoru F' ve své podstatě vyjadřuje poměr mezi dvěma tepelnými odpory, ve jmenovateli je obsažen odpor proti přenosu tepla z kapaliny do okolního vzduchu, v čitateli je odpor proti přenosu tepla z absorbéru do okolního vzduchu. Účinnostní součinitel kolektoru je konstantní pro danou konstrukci absorbéru a průtok teplonosné látky. Pro různé konstrukční řešení spoje lamely a trubky se liší vztah pro stanovení F' [2]. Vztah (13) platí pro typ konstrukce absorbéru zobrazený na obr. 3. Rovnici účinnosti solárního kolektoru v závislosti na střední teplotě teplonosné látky Tm lze psát jako
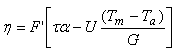 | (14) |
Z účinnostního součinitele kolektoru F' vyplývají důležité zásady návrhu konstrukce kolektoru, zejména absorbéru. Se zmenšováním rozteče trubek W v kolektoru a tedy zmenšováním šířky lamely se zvyšuje účinnostní součinitel kolektoru, stejně jako se zvětšující se tloušťkou lamely δ a zvyšující se tepelnou vodivostí materiálu lamely a trubky. Omezení tloušťky absorbéru vyplývá z ekonomiky návrhu absorbéru a snahy o minimalizaci tepelné kapacity (setrvačnosti) kolektoru. Je samozřejmé, že účinnostní součinitel kolektoru se bude zvyšovat také se snižujícím se celkovým součinitelem prostupu tepla kolektoru U a zvyšujícím se součinitelem přestupu tepla z povrchu trubky do teplonosné látky hf,i (ovlivněno především rychlostí proudění teplonosné látky v trubce).
Využitelný tepelný tok vztažený na jednotku délky trubky se celý přenáší do teplonosné látky. Ta vstupuje do kolektoru o teplotě Tin, zvyšuje svou teplotu a opouští kolektor o teplotě Te. Energetickou bilancí elementu teplonosné látky lze získat diferenciální rovnici, jejímž řešením je závislost teploty teplonosné látky na souřadnici ve směru toku. Dosazením okrajové podmínky získáme vztah pro stanovení výstupní teploty Te z kolektoru v závislosti na jeho parametrech a provozních podmínkách.
| (15) |
kde ![]() (kg/s) je hmotnostní průtok teplonosné látky kolektorem a c (J/kg.K) je měrná tepelná kapacita teplonosné látky.
(kg/s) je hmotnostní průtok teplonosné látky kolektorem a c (J/kg.K) je měrná tepelná kapacita teplonosné látky.
Při hodnocení provozu solárních kolektorů je výhodné pracovat s veličinou, která vztahuje energii dodanou solárním kolektorem (okamžitý využitelný tepelný zisk) k energii, která by byla dodána za předpokladu, že by teplota celého absorbéru byla rovna vstupní teplotě teplonosné látky. Tato veličina se nazývá tepelný přenosový součinitel kolektoru FR (-).
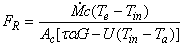 | (16) |
Dosazením z rovnice (15) lze tepelný přenosový součinitel kolektoru vyjádřit jako
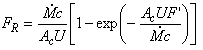 | (17) |
Pro účely grafických zobrazení je dále definován průtokový součinitel kolektoru F" (-) jako poměr FR k F'.
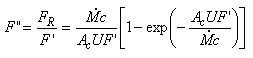 | (18) |
Průtokový součinitel kolektoru představuje poměr energie dodané solárním kolektorem k energii, která by byla dodána za předpokladu, že průměrná teplota teplonosné látky v kolektoru je rovna vstupní teplotě. Průtokový součinitel kolektoru je funkcí jediné bezrozměrné proměnné.
Na obr. 4 je znázorněna závislost součinitelů F, F' a FR na tepelné vodivosti žebra a trubky s vyznačením oblasti různých materiálů používaných pro absorbéry kolektorů (ocel, hliník, měď). Z grafu je zřejmá silná vazba součinitelů na volbu použitého materiálu.
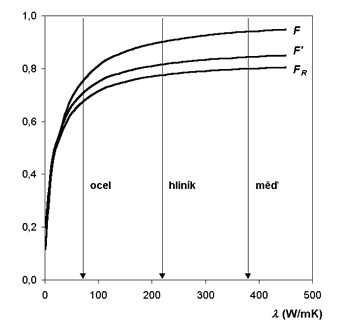
Obr. 4 - Závislost součinitelů F, F' a FR na tepelné vodivosti materiálu absorbéru λ
Tepelný přenosový součinitel kolektoru FR je závislý na průtoku a na vlastnostech teplonosné látky (hustota, tepelná kapacita). Zvyšováním průtoku v kolektoru se snižuje teplotní spád na kolektoru (rozdíl mezi výstupem a vstupem), střední teplota v kolektoru se přibližuje teplotě na vstupu a přenosový součinitel kolektoru roste. Roste tím samozřejmě i účinnost, neboť při nižší střední teplotě absorbéru jsou tepelné ztráty do okolí nižší.
Při nárůstu průtoku nade všechny meze je teplotní rozdíl mezi vstupem a výstupem kolektoru roven nule, ale povrch absorbéru má teplotu vždy vyšší než je teplota teplonosné látky. Tento rozdíl teplot je vyjádřen účinnostním součinitelem kolektoru F'. Proto tepelný přenosový součinitel kolektoru FR je vždy menší než účinnostní součinitel kolektoru F'.
Tepelný přenosový součinitel kolektoru FR je svým významem ekvivalentní účinnosti tepelného výměníku, definovaného jako poměr okamžitého přeneseného tepelného výkonu k maximálnímu možnému tepelnému výkonu. V solárním kolektoru dochází k maximálnímu možnému využitelnému výkonu v případě, že celý kolektor je na teplotě rovné teplotě vstupující látky. Tento maximální možný využitelný výkon násobený (korigovaný) přenosovým součinitelem kolektoru FR dává okamžitý využitelný tepelný výkon (skutečně dodanou energii) podle vztahu
| (19) |
a podobně pro účinnost
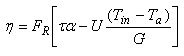 | (20) |
kde (Tin - Ta)/G je střední redukovaný teplotní rozdíl stanovený pro vstup do kolektoru.
Uvedené rovnice jsou vhodné pro práci v podstatě se všemi plochými kolektory. Využitelný tepelný výkon z kolektoru lze stanovit jako funkci teploty na vstupu do kolektoru Tin. Křivku účinnosti kolektoru v závislosti na vstupní teplotě lze výhodně použít při matematickém modelování solárních soustav, neboť teplota na vstupu do kolektoru Tin je obvykle známa, na rozdíl od střední teploty absorbéru Tabs či střední teploty teplonosné látky Tm (přepokládá znalost teploty na výstupu kolektoru Te). Matematický model kolektoru se potom chová jako fyzikální model (reálný kolektor při experimentu): na základě znalosti teploty a průtoku na vstupu do kolektoru a klimatických veličin je možné stanovit teplotu na výstupu z kolektoru, užitečný výkon odebíraný z kolektoru a účinnost kolektoru.
Pro hodnocení výkonu, resp. účinnosti solárních kolektorů je třeba znát hodnoty celkového součinitele přenosu tepla kolektoru U a součinitele přestupu tepla uvnitř trubek kolektoru hf,i. Ty jsou však do určité míry funkcí teploty. Střední teplotu teplonosné látky v kolektoru Tm lze určit ze vztahu
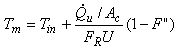 | (21) |
Tato teplota je vhodná pro stanovení teplotně závislých vlastností teplonosné látky v kolektoru.
Střední teplotu absorbéru Tabs určíme jako
| (22) |
Energetickou bilanci je nutné řešit v iteračním cyklu, neboť celkový součinitel prostupu tepla kolektoru U je zpětně závislý na Tabs.
LITERATURA
[1] Cihelka, J.: Solární tepelná technika. T. Malina 1994.
[2] Duffie, J., Beckman, W.: Solar Engineering of Thermal Processes. 2nd edition. John Wiley & Sons, Inc. 1991. ISBN 0-471-51056-4.
[3] Kreider, J., Kreith, F.: Solar Energy Handbook. McGraw-Hill, Inc. 1981. ISBN 0-07-035474-X.
[4] ČSN EN ISO 9488 - Solární energie - Slovník. ČSNI 1998.
[5] ČSN EN 12975-2 - Solární tepelné soustavy a součásti - Solární kolektory - Část 2: Zkušební metody. ČSNI 2003.
[6] Matuška, T.: Aktivní solární tepelné systémy - část 1. Teoretické vztahy. Vytápění, větrání, instalace. 2003, roč. 12, č. 2, s. 64-67. ISSN 1210-1389.